In Pearl's book "Causality" on page 124 (http://bayes.cs.ucla.edu/BOOK-2K/ch3-3.pdf) he says:
A set of variables $Z$ satisfies the back-door criterion relative to an ordered pair $(X_i,X_j)$ in a DAG G if:
(i) no node in $Z$ is a descendant of $X_i$; and
(ii) $Z$ blocks every path between $X_i$ and $X_j$ that contains an arrow into $X_i$
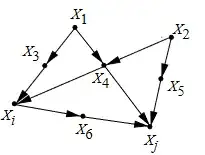
Then, he gives the example graph:
And he says that $Z_1=\{X_3,X_4\}$ and $Z_2=\{X_4,X_5\}$ satisfy the back-door criterion but $Z_3=\{X_4\}$ does not because it does not block $(X_i,X_3,X_1,X_4,X_2,X_5,X_j)$.
But, this does not make sense to me. The path Pearl mentions goes through $X_4$ which is in $Z_3$ so this confused me. In fact, it seems to that $Z$ satisfies the back-door criterion relative to $(X_i,X_j)$ IFF $X_4\in Z$.
Am I totally missing something? It almost feels like I've gotten the definition totally wrong in my head.