I've got some simulation data which I'm trying to use to fit some historical data (red points). The simulation isn't a nice function $f(t, a, b, c...)$, instead it's just the result of numerically simulating a system. Is reasonable to take the nearest points in my simulation to each red point, and use these to calculate $\chi^2$ values to compare one simulation to another? Normally in physics we would use the number of parameters in the model to calculate reduced $\chi^2$ using degrees of freedom but I'm not really sure what my degrees of freedom are here. I use the initial and final condition so fix the bounds of my model, so perhaps $\nu = N_{\textrm{points}} - 2$?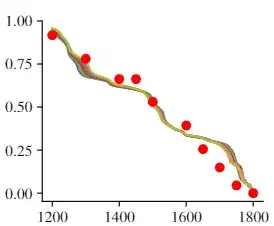
If $\chi^2$ isn't appropriate, is there some other way I can quantify the goodness of fit of my various simulations?