I have a random variable X, number of hours that kids from 10-12 years old spend on video games in one month in a specific country, and I want to test the hypothesis that the mean of my population $u_{x}$ is higher than 50hours. I have a sample with size 5000 where each data point shows me the number of hours that a different kid (10-12 years old) spent on video games. I constructed my hypothesis as
$H_{o}: u_{x} = 50$
$H_{a}: u_{x} > 50$
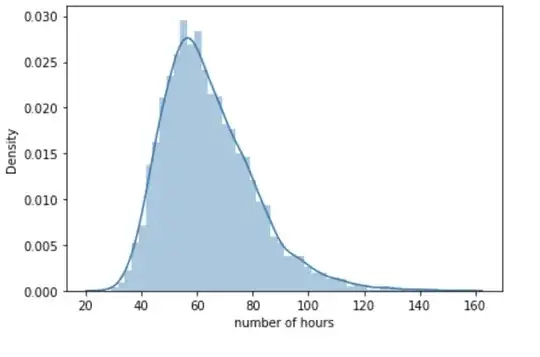
To test this hypothesis, I want to use one sample t-test because I don’t know the population variance. I know that one of the assumptions of t-test is that the population should have a normal distribution. When I draw the distribution of my sample, I have the below plot.
When I run Shapiro-Wilk Test for normality usin my sample, I reject the null hypothesis, my sample is not drawn from a population with a normal distribution. Under these circumstances shouldnt I use one-sample t-test but rather should I use a non-parametric test, if so which test (maybe Wilcoxon Rank Sum test)? Or since I have a sample size 5000, can I simply ignore the normality assumption and continue with one-sample t-test (from T-test for non normal when N>50? discussion, I feel like continuing with t-test is still safe)?
Thank you!