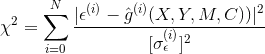If you look at basic resources on R-squared, such as https://en.wikipedia.org/wiki/Coefficient_of_determination, they all tend to say the same thing: That it is a measure "about the goodness of fit of a model." However, when dealing with linear regressions that have a low absolute slope, that doesn't seem to (entirely) be the case.
Here's a dataset with 100 points drawn from a standard normal distribution. The values have been slightly tweaked so that the linear fit is exactly $y=0$:
$R^2$ for the linear regression will be 0, which follows directly from the definition: Because the model is exactly the same as the mean (both are 0), the squared error of both is the same in all cases. However, both from eyeballing the result and from understanding the source of the data, we know that the linear regression is actually a good fit, despite the worst-possible R-squared of 0.
In contrast, if we bias the data with a component of $\frac{x}{10}$, we get the 2nd part of the graph. The linear fit to this biased data is $R^2 \approx 0.89303$, despite it fitting no better (or worse) than the original data - all that's happened is the addition of a small slope.
So it seems clear that $R^2$ is actually very sensitive to the slope of the fit, not just the goodness of the fit. Is this well-known/discussed anywhere? Or am I missing something in this analysis?