Typically, people will use Fisher's z-transformation (arctan) to turn the r into a variable that is approximately normally distributed. When I look though his paper published in 1915(https://www.jstor.org/stable/2331838), i couldn't understand how he reduced dx1dy1dx2dy2 to the simple parts: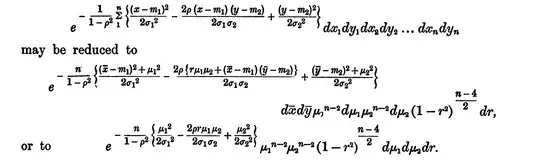
Asked
Active
Viewed 40 times
1
黄文戈
- 11
- 3
-
Fisher's Z is the *hyperbolic* arctangent, not the arctangent. A geometrical explanation of what Fisher is doing here is given at https://stats.stackexchange.com/a/85977/919. Also see https://stats.stackexchange.com/a/151969/919 for an account of Fisher's paper in terms of a change to cylindrical coordinates. – whuber Apr 12 '21 at 16:25
-
Thank you for your answer! – 黄文戈 Apr 13 '21 at 23:56
-
@whuber Hi, after I read the link you given, I still can't not understand how fisher reduced the 2n dimension equation to the simple 3 dimension part. And though I saw the geometrical explanation of what Fisher is doing, It was a little abstract for me to imagine in N parts of (xi, yi) space. I will really appreciate if you can explain how fisher reduced this equation. – 黄文戈 Apr 16 '21 at 05:33
-
He integrated over the surface of the sphere. – whuber Apr 16 '21 at 13:28