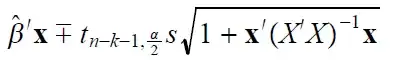(1) I assume you want to test $H_0: p=.5$ vs. $H_a: p>.5.$ Under $H_0,$
the number of successes is $X \sim \mathsf{Binom}(n=408, p=.5),$ and the
P-value of this right-tailed test is
$$P(X \ge 178\,|\,H_0) = 1 - P(X\le 177\,|\,H_0) = 0.0037 < 0.05$$,
by an exact binomial computation in R (below), so you will reject $H_0$
in favor of $H_a$ at the 5% level (also at the 0.5% level).
1 - pbinom(177, 308, .5)
[1] 0.003652809
Your estimate $\hat p \approx 0.55$ of the success probability $p$ is incorrect,
it should be $\hat p = 178/308 = 0.578.$
Unless you are regularly using technology such as a statistical calculator
or statistical computer software, in your course, I don't suppose you are expected to compute
the exact binomial P-value.
Perhaps, you are supposed to get a normal approximation
to $X$ by using $\mathsf{Norm}(\mu, \sigma),$ where (under $H_0)$ $\mu = 308(.5) = 154,
\sigma = \sqrt{208(.25)} = 8.775).$ Then you can find
$P(X \ge 177.5\,|\,H_0) \approx 0.0037$ by
standardizing and using printed tables of the standard normal CDF.
I will leave the details of that to you.
(2) You can do a two-sample t test if you have sample sizes, means, and standard deviations---along with the knowledge that your observations are a random sample from a (nearly)
normal distribution. (The correct notation for the two sample means would be
$\bar X_1 = 3.5; \bar X_2 = 3.37,$ and you are missing the required standard deviations.)
However, you say the normality criterion is violated, so you
would need to do a nonparametric test to compare the centers of the two distributions.
If the samples are of about the same shape, you could use a two-sample Wilcoxon rank sum test. And for that you would need to have the $n_1 = n_2 = 308$ observation from
the two samples.
Suppose I have samples x1 and x2 (both of size 308) in R, with descriptive statistics as below:
summary(x1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.6899 2.5553 3.2400 3.5036 4.1538 8.0909
summary(x2)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.191 2.626 3.436 3.580 4.357 9.066
Boxplots of the two samples are shown below. They are noticeably right-skewed. Enough so, that I would not want compare them with a t test. (Also, both are rejected as normal by Shapiro-Wilk tests, with very small P-values; not shown.) More important, the medians (vertical bars within boxes) do not differ by much compared with the large variability of the two samples.
boxplot(x1, x2, horizontal=T, col="skyblue2")
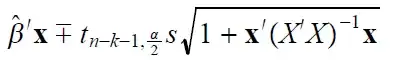
Because shapes of the samples are very similar, it seems appropriate to use a 2-sample Wilcoxon test to see if one sample is significantly shifted relative to the other.
(Roughly speaking, we might say we are comparing the two sample medians for significance.) The P-value is well above 0.05, so the null hypothesis of equal medians
is not rejected.
wilcox.test(x1, x2)
Wilcoxon rank sum test with continuity correction
data: x1 and x2
W = 45006, p-value = 0.2721
alternative hypothesis: true location shift is not equal to 0
Of course, these are my fake data sampled in R. It is possible that two-sample Wilcoxon test for your real data, if you have them available, would show a significant difference (on account of considerably less variability).