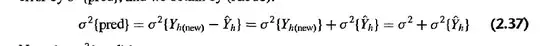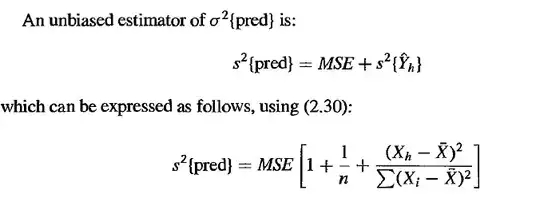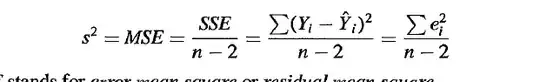The following question is from Kutner's Applied Linear Statistical Models - Ch 2 - 2.12
To answer the question a few pieces of information are needed, provided below:
What I gather the question is asking me is that if I take the limit as $n \to \infty$ then what happens to the variance of my new prediction?
Now clearly based on the expressions below, it would appear that in both cases $Var(pred)$ and $Var(\hat{Y_{h}})$ would both be $0$. And as such they can be brought increasingly close to $0$.
But the solution says that this is not the case and I'm wondering why? Is it because they specified the theoretical variances? i.e $\sigma^{2}(pred)$ and $\sigma^{2}(\hat{Y_{h}})$ and I took the estimates by using the sample variances for the respective pieces? But even still the theoretical variances still involve having an $n$ in the denominator.....Am I looking at something wrong?