Why does this criterion characterize the median of a continuous random variable?

Question

If $X$ is a continuous random variable, then let

$$\min_a{\mathbb{E}\:| X - a |} = \mathbb{E}\: | X - m |$$

Why is $m$ the median of $X$?

Answer 1

When $a$ is a local minimum of $\mathbb{E}|X-a|$, that means for sufficiently small $\varepsilon$ the value of this expectation will not decrease when $a$ is changed to $a + \varepsilon$:

$$0 \le \mathbb{E}|X-(a+\varepsilon)| - \mathbb{E}|X-a| = \mathbb{E}[|X-(a+\varepsilon)| - |X-a|].$$

Consider the case where $\varepsilon \ge 0$. The argument of the right hand side equals $\varepsilon$ for $X \le a$, $-\varepsilon$ for $X \ge a+\varepsilon$, and otherwise has magnitude less than $\varepsilon$.

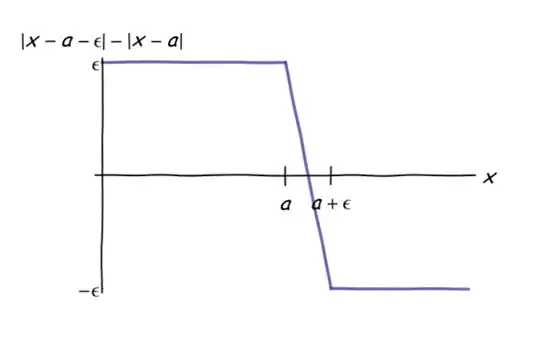
Therefore, letting $F$ be the CDF of $X$ and integrating, it is now evident that the right hand side is the sum of three things:

1. $\varepsilon F(a)$ coming from $X \le a$,

2. $-\varepsilon (1-F(a+\varepsilon))$ coming from $X \ge a$, and

3. Something less than $\varepsilon(F(a+\varepsilon) - F(a))$ coming from $a \lt X \lt a+\varepsilon$.

The continuity assumption for the distribution of $X$, which amounts to assuming $F$ is differentiable, is tantamount to saying that the third part equals $F'(a)\varepsilon^2 + o(\varepsilon^2)$. Similarly, the second part can be expanded

$$-\varepsilon (1-F(a+\varepsilon)) = \varepsilon(F(a)-1) + F'(a)\varepsilon^2 + o(\varepsilon^2).$$

Adding all three up yields

$$0 \le \mathbb{E}[|X-(a+\varepsilon)| - |X-a|] = \varepsilon(2F(a)-1) + O(\varepsilon^2).$$

It should be evident that the same result holds when $\varepsilon \lt 0$. (Just apply the preceding result to the variable $-X$.)

This inequality can be true for arbitrarily small $\varepsilon$ if and only if the coefficient of $\varepsilon$ is zero, whence

$$2F(a) - 1=0.$$

Accordingly, at any local minimum $a^*$, $F(a^*) = 1/2$. That defines a median. (Note that the median might not be unique: if $F$ is constant in a neighborhood of a median, all values in that neighborhood will be local minima.)

Answer 2

Here's a simple conceptual explanation. You want to park your car and walk to two different stores. If you park anywhere on the line between them, your total walking distance will be minimized because if you move the car the distance to one store will increase by exactly the amount that the distance to the other decreases. If you park beyond either store (on the extension of that line) you'll have to walk further.

Now add another two stores and think about it the same way. If you have an odd number of stores, you'll park in the middle one and the total distances to the others will be minimized. (The store owner may get upset but we're doing a thought experiment here.)

Answer 3

A faster resolution of the minimisation is based on the representation (by an integration by part) $$\int_0^\infty x \text{d}F(x)=\int_0^\infty (1-F(x))\text{d}x$$ which leads to \begin{align*}\mathbb{E}[|X-a|]&=\int_{-\infty}^a (a-x) \text{d}F(x)+\int^{\infty}_a (x-a) \text{d}F(x)\\&=\int_{-\infty}^a F(x) \text{d}x+\int^{\infty}_a (1-F(x)) \text{d}x\\ \end{align*} Differentiating in $a$ and setting the value to zero leads to the equation $$F(a)-(1-F(a))=0$$that is$$F(a)=\frac{1}{2}$$