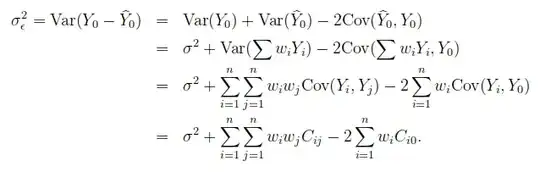Background
I am currently working on a problem to study the dynamics of aggregate losses in some state-owned companies in my country. I was successful in gathering data of losses across 34 such companies for 9 years. Distribution of losses across companies for year - 1 was fit using MATLAB's distribution fitting tool (I selected the distribution using visual inspection and selecting the one with lease standard error). A similar exercise was carried out for 9 years. It was observed that across years, the distribution type remained constant, only shape and scale parameters were changing. This distribution was a t - Location - Scale Distribution belonging to the Location - Scale family of curves. The PDF of said distribution is given by:
$$ T = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sigma \sqrt{\nu \pi} \Gamma\left(\frac{\nu}{2}\right)}\left[\frac{\nu+\left(\frac{x-\mu}{\sigma}\right)^{2}}{\nu}\right]^{-\left(\frac{\nu+1}{2}\right)} $$
The Problem
The aforementioned distribution has been observed to be changing with time - i.e., every year, the shape and scale parameters of the distribution of losses across companies change. I wish to forecast this distribution for the next year.
- How can I forecast the dynamics of the distribution change?
- Can I commit to simply extrapolating the shape and scale parameters for the distribution?
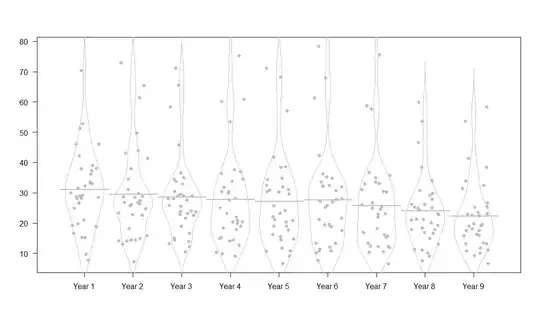
- Am I correct in inferring that the distribution is indeed changing with time? (See attached figure of the distributions) If I am not correct on the said inference, are there tests I can do to see if the change in time is not just an artifact of low availability of data?
- How correct would I be to say that the losses are varying both in space (here different companies) and in time? Could I look at state-space approaches for forecasting?
Any and all feedback is welcome. I am very new to forecasting as my discipline did not involve such rigorous statistical modelling. Please correct me wherever I need to be corrected. Following is the data for the said losses. Each column is the loss of 34 utilities. Each row, hence, is the loss incurred by a singular utility over 9 years.
9.6900 14.5100 10.5300 9.9000 6.5700 7.6700 6.5600 7.4800 11.1800
16.6300 14.2000 12.1900 12.7400 11.7700 12.0100 17.0200 17.0200 16.0400
52.9300 61.4500 65.5500 60.2600 68.2000 67.8300 57.7400 53.6400 58.3600
29.0300 28.7100 29.4700 31.8500 30.2500 25.8400 25.0200 20.1000 17.6400
37.9800 28.8400 29.0500 25.1200 23.1700 27.8400 26.6900 20.9900 18.0800
19.8300 15.8000 16.6500 15.1600 16.1900 10.7600 13.2900 11.1300 10.0300
28.6300 18.1300 25.5400 17.9400 15.5100 19.6800 15.3900 12.9900 10.8300
7.7600 14.0800 15.1200 14.1400 10.7200 13.3100 16.8100 24.3300 13.5200
15.2300 13.0800 13.1400 10.4000 10.8300 10.8100 10.4100 10.1800 6.6000
15.2700 14.8300 14.4000 14.9400 14.7700 11.4700 10.5900 11.2400 11.7200
32.3500 26.7500 28.0300 30.4100 24.1200 25.1800 24.6500 21.1500 19.6400
18.8900 7.2000 14.0100 14.3700 9.1000 10.2100 12.2100 9.1000 9.3100
28.1100 26.2900 27.5300 28.3100 30.8900 30.7100 30.2300 23.1000 19.1600
29.9100 29.8500 29.0600 36.9700 38.6100 34.8300 35.0300 30.6700 25.3800
70.4400 72.8600 71.1600 60.8700 57.0200 61.2700 58.7500 59.9700 53.6700
21.1000 22.7500 22.5700 20.4500 18.9300 17.5900 12.3700 14.9100 13.1700
28.2100 28.7300 28.9900 30.4200 17.6700 21.6400 11.9900 19.2700 13.2000
38.0500 25.7500 23.9600 18.2800 30.4500 21.2500 18.2400 17.8600 16.3900
28.5100 26.2200 23.6200 20.4400 20.4200 19.4900 16.2300 18.2900 22.8400
42.2600 43.9500 45.8500 29.9700 29.6000 32.4700 33.5900 34.0400 38.3700
36.1600 31.1200 34.4300 28.1600 21.1500 32.3800 30.3700 17.8700 17.5200
46.1100 37.9900 34.9400 36.4000 34.8300 27.0900 26.0900 26.1800 33.9500
25.0200 23.3000 21.6300 21.9500 14.3900 19.2500 23.1200 22.7300 18.9700
38.9900 43.0900 36.5900 27.5500 32.5300 33.5100 32.9600 24.9800 22.4400
46.1500 49.7300 22.8500 75.3000 38.3700 78.4800 75.5600 38.5000 41.3600
19.3500 14.4300 18.9100 9.1300 20.9300 13.3400 21.9500 21.3400 19.7700
33.0400 26.8000 28.1200 19.9000 22.0600 28.1300 25.6200 25.1900 23.0900
31.5100 22.5500 23.8300 18.9700 25.7100 26.9900 22.9000 26.1600 23.4700
26.6800 24.7300 23.1800 20.9100 31.0800 32.0000 33.0800 29.7900 25.1800
51.3500 65.4600 58.3200 53.5100 71.2300 42.3700 36.6800 46.5200 32.4800
29.1600 34.4800 33.7600 33.8500 41.8100 36.2300 35.7700 29.2000 31.3400
37.3700 41.4500 30.4800 37.6100 34.2900 32.1600 15.6400 25.1000 22.5300
33.5300 28.4800 25.8400 23.1800 19.0100 18.8200 12.2500 16.6800 15.7900
33.2400 27.4000 32.9000 34.4300 32.0500 35.3500 31.1000 27.9200 26.7400