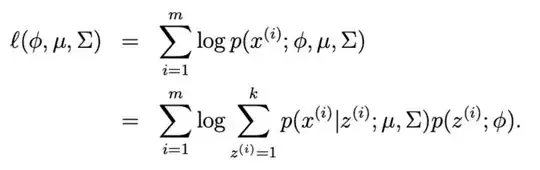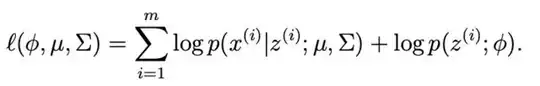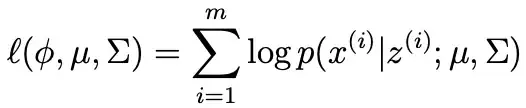About the derivation of EM for mixture of Gaussians

Question

I'm reading Andrew Ng's note about Mixtures of Gaussians and the EM algorithm

He writes the likelihood of data as

where random variables $z^{(i)}$'s indicate which of the $k$ Gaussians each $x^{(i)}$ had come from. Then he says that if we knew what the $z^{(i)}$'s were, the maximum likelihood problem would have been easy. Specifically, we could then write down the likelihood as

I could not get this last step. If we knew what the $z^{(i)}$'s were, then shouldn't we just need to calculate the likelihood from the Gaussian distribution (I understand that if we knew $z^{(i)}$'s we do not need to take a weighted sum over $k$ Gaussians but why do we still need to multiply with the probability of the known $z^{(i)}$, i.e., $p(z^{(i)};\phi)$)? In other words shouldn't the likelihood be as below:

There is a similar question here but it does not answer my question.

Answer 1

What I understand Andrew Ng is saying is the following:

We want to derive estimates of the parameters by solving for $\phi, \mu, \Sigma$. We do this by maximising $l(\phi, \mu, \Sigma)$ i.e. the log likelihood of the observed data $x^{(i)}$ w.r.t to the parameters. However, there are latent variables $z^{(i)}$, which complicate matters.

Ideally, we would like to do the following:

$$\begin{align}\phi^*, \mu^*, \Sigma^* &= \text{argmax}_{\phi, \mu, \Sigma} \sum^m_{i=1} \log p(x^{(i)}; \phi, \mu, \Sigma) \\ &= \text{argmax}_{\phi, \mu, \Sigma} \sum^m_{i=1} \log \sum^k_{z^{(i)} = 1} p(x^{(i)}, z^{(i)}; \phi, \mu, \Sigma) \\ \end{align}$$

I.e. Maximising the log-likelihood of the observed data, after having marginalised out the latent variables $z^{(i)}$ over all $k$ states in the joint distribution.

What he means by:

However, if we set to zero the derivatives of this formula with respect to the parameters and try to solve, we’ll find that it is not possible to find the maximum likelihood estimates of the parameters in closed form. (Try this yourself at home.)

Is that it is difficult to maximise the expression due to maximising a $\log(\sum)$ term, that is, a summation contained within a log. Frequently in ML you will find that this a difficulty encountered with latent variable models, which is what necessitates EM.

Now imagine if $z^{(i)}$ were also observed data. The log-likelihood of the observed data, that is both $x^{(i)}$ and $z^{(i)}$, is the log of the joint distribution evaluated at $x^{(i)}$ and $z^{(i)}$, where the latter is now known.

So in this case, as the log-likelihood is just a function of the parameters, our maximisation problem would be:

$$\begin{align}\phi^*, \mu^*, \Sigma^* &= \text{argmax}_{\phi, \mu, \Sigma} \sum^m_{i=1} \log p(x^{(i)}, z^{(i)}; \phi, \mu, \Sigma) \\ &= \text{argmax}_{\phi, \mu, \Sigma} \sum^m_{i=1} \log \left( p(x^{(i)} | z^{(i)}; \mu, \Sigma) p (z^{(i)}; \phi)\right) \\ &= \text{argmax}_{\phi, \mu, \Sigma} \sum^m_{i=1} \log p(x^{(i)} | z^{(i)}; \mu, \Sigma) + \log p (z^{(i)}; \phi)\\ \end{align}$$

However, we cannot do this because the $z^{(i)}$ are not actually known.

To close, there are two takeaways in my opinion:

1. That $\log(\sum)$ is difficult to maximise when the arguments which you are maximising with respect to are inside the summation.

2. That the presence of latent variables complicates maximum likelihood estimation, thereby necessitating techniques such as EM.

---

Just read this back to myself and realised I may have missed the point of your question.

The reason why you care about $p(z^{(i)}; \phi)$ is in Ng's language, you are have specified a generative model $p(x, z)$ rather than a discriminative model, although applied to unsupervised density estimation rather than supervised learning. If that is somewhat unclear just prompt below and I will edit.