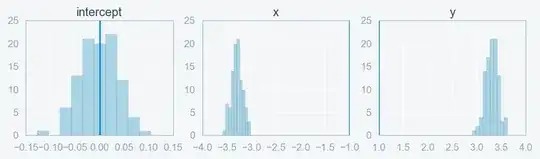
I am trying to replicate one of the images from this post.
In particular I want to plot something similar to this image in matlab:
I.e. I want these three differently peaked distributions, where the tails are very clear. Can someone help me with such a plot?
Code as of now:
y = normpdf(x,0,1);
plot(x,y)
y1 = tpdf(x,5);
hold on
plot(x,y1)
hold on
y2 = tpdf(x,1000)