Interpretation of interaction effects when the confidence interval of the main effect includes zero

Question

This post might sound similar to some previous posts, such as this one or the ones here, but none could help me.

I'm using a mixed-effect model to assess the association between individual practices and career success. I use 12 variables to measure individual practices at a different point in time. Each observation corresponds to a career trajectory of one individual in specific career age. I divide each career into three categories: 1) early-career, 2) mid-career, 3) and late-career (IV: career_stage). I am interested to understand if the patterns of successful career changes in different career stages. In other words, if certain practices are likely to be more beneficial in certain career stages. To do this, I look at the interaction of career_stage and all other covariates.

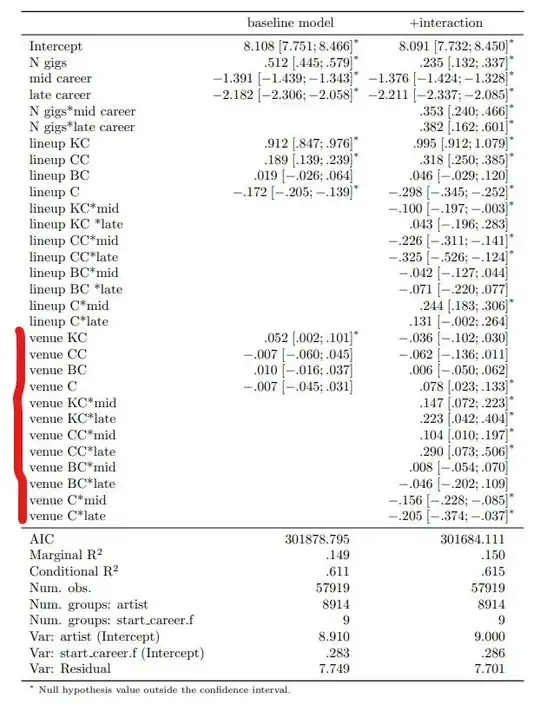
The problem arises when the confidence interval of the main effect for some variables includes zero. That means I can make any decision about the direction of the effect. These are highlighted variables in the table below.

but the interaction effects are positive, and their CI do not include zeros. This still allows me to make some interpretations. For example, in the case of venue KC, I can say the association of the variable and success increase over career stages compared to the early career. But how do I make any claim about the marginal effect? I want to know if I can say: "on average association of the variable X with success is positive or negative" if the direction of main effect was known, I could sum up the two cofficients, for example -.036+147 and conclude there is a positive association between venue KC and success in mid career.

When I look at the interaction plots, it seems that association is slightly negative for the early careers, but it is positive for the mid and late careers. However, I'm not sure if it's the right way to read this plot. And if so, how can I see it on the table. [y-axis: travel dist log= success, x-axis: kcore venue= KC venue ]

Answer 1

When there are interaction terms, you have to be careful about how you interpret p-values and confidence intervals for what you call a "main effect." Each "main effect" represents the association of the corresponding predictor with outcome when all the other predictors are at their reference levels.

A predictor having an "insignificant" coefficient of 0 under those reference conditions but also involved in interactions could well have a "significant" association with outcome when the other predictors take on alternate values of interest. Something so simple as centering one predictor can affect the apparent "significance" (difference from 0) of the "main effects" of all predictors with which it interacts. Thus there is no single "main effect" that fairly represents the association of a predictor with outcome if it is involved in an interaction.

But how do I make any claim about the marginal effect?

You have to be particularly cautious when you wish to make claims about marginal estimates when there are interactions. Such claims might not at all be helpful. This recent answer (from the author of widely used software to estimate marginal means) notes the dangers of relying on them in observational studies when there are substantial interactions:

If, on the other hand, we do have sizeable interaction effects, then (as our forebears recommend) we simply should not even consider estimating marginal means.

Showing illustrative predictions (and error estimates) from your model under specific situations of interest will be much more useful when there are interactions.