Apologies if this question is too simplistic but I really couldn't find an answer for it on stats or math stackexchange.
Considering the simple linear regression (sum of least squares) for bivariate data.
We can get a simple linear regression by one of two methods:
- Considering x as an independent variable and y as dependent. (i.e. Y on X)
- Considering y as an independent variable and x as dependent. (i.e. X on Y)
Since the simple linear regression of Y on X can be expressed in following form
$y=\alpha_{yx}+\beta_{yx} x$ provided that $\sum_{i=1}^n (y_i - \alpha_{yx} - \beta_{yx} x_i)^2 \rightarrow min$
and similarily for X on Y
$x=\alpha_{xy}+\beta_{xy}y$ provided that $\sum_{i=1}^n (x_i - \alpha_{xy} - \beta_{xy} y_i)^2 \rightarrow min$
I interpreted the second case of y being the independent variable to be the same as plotting the values of y on the horizontal and x on the vertical. (if this is wrong then all that follows is wrong so please correct me)
Would it then, be correct to say that the linear simple regression as calculated for Y on X can be transformed to the case of X on Y by simply taking the vector associated with the line of best fit and (first) rotating it 90° counterclockwise and flipping it along the vertical axis?
I have tried to illustrate this with the following diagram.
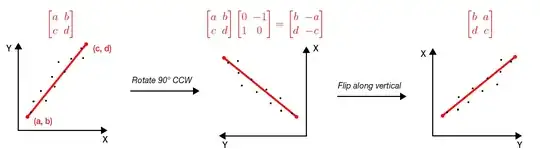
This process can also be achieved by simply multiplying the first matrix by $ \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$
Is this method of thinking correct or have I misunderstood something about simple linear regression? I wasn't able to clearly explain this doubt to my prof and its been nagging me ever since.
Would greatly appreciate any and all input.