2

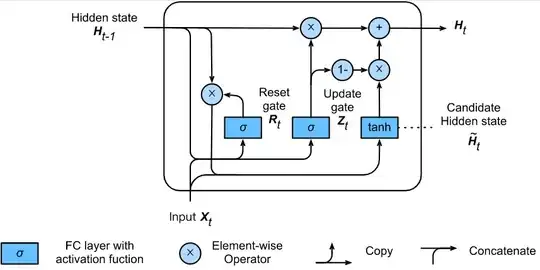
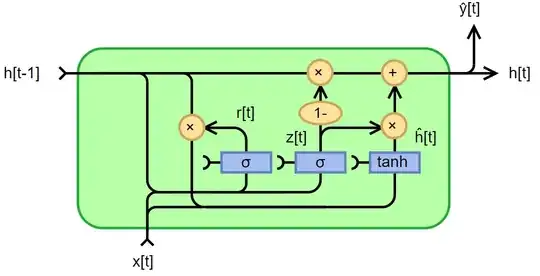
Looking into GRU equation I see 2 type for final output. One is from, https://d2l.ai/chapter_recurrent-modern/gru.html#hidden-state, that is,

$ \mathbf{R}_t = \sigma(\mathbf{X}_t \mathbf{W}_{xr} + \mathbf{H}_{t-1} \mathbf{W}_{hr} + \mathbf{b}_r) \\ \mathbf{Z}_t = \sigma(\mathbf{X}_t \mathbf{W}_{xz} + \mathbf{H}_{t-1} \mathbf{W}_{hz} + \mathbf{b}_z) \\ \tilde{\mathbf{H}}_t = \tanh(\mathbf{X}_t \mathbf{W}_{xh} + \left(\mathbf{R}_t \odot \mathbf{H}_{t-1}\right) \mathbf{W}_{hh} + \mathbf{b}_h) \\ \mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t $

enter image description here

There it is mentioned,

whenever the update gate $Z_t$ is close to 1, we simply retain the old state. In this case the information from $X_t$ is essentially ignored, effectively skipping time step t in the dependency chain. In contrast, whenever $Z_t$ is close to 0, the new latent state $H_t$ approaches the candidate latent state $\tilde{H}_t$ .

Another one from Wikipedia,

$ z_{t} = \sigma _{g}(W_{z}x_{t}+U_{z}h_{t-1}+b_{z}) \\ r_{t} =\sigma _{g}(W_{r}x_{t}+U_{r}h_{t-1}+b_{r}) \\ {\hat {h}}_{t} =\phi _{h}(W_{h}x_{t}+U_{h}(r_{t}\odot h_{t-1})+b_{h}) \\ h_{t} =(1-z_{t})\odot h_{t-1}+z_{t}\odot {\hat {h}}_{t} $

enter image description here

They both produce different values when working with sample vectors. My question is, are they both correct and if so is there any particular reason the first equation is implemented in major Deep Learning libraries?

My confusion is between, $\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t$ and $\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{\tilde{H}}_{t} + (1 - \mathbf{Z}_t) \odot \mathbf{H}_{t-1}$. In the latter equation when $Z_t$ is close to 1 then the new latent state $H_t$ approaches the candidate latent state $\tilde{H}_t$. It is doing opposite of what is mentioned previously.

Following keras and pytorch implementation it seems, $\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_t$ is implemented on code.

B200011011
  • 121
  • 5

1 Answers1

1

They are both correct and equivalent in the sense that the cell can learn the same function.

The gating is done using a sigmoid function and it holds $\sigma(x) = 1 - \sigma(-x)$, so you can switch between the formulations by negating the weights in the $z_t$ gate computation.

Jindřich
  • 2,261
  • 4
  • 16
  • The output value of first formula `H_t` and `h_t` in the second don't match if working with same sample input and weights. So in case of second formula do I have to use formula, $z_{t} = \sigma _{g}(-(W_{z}x_{t}+U_{z}h_{t-1}+b_{z}))$? – B200011011 Mar 04 '21 at 09:56
  • Yes, exactly like this. – Jindřich Mar 04 '21 at 10:17
  • Upvoted for meaningful answer, but won't accept as it is not clear to me why the negation is not shown in second the formula to make them equivalent. – B200011011 Mar 04 '21 at 17:01