Minimum expectation

Question

The random variable $X$ has a continuous distribution. For an increasing density function $f(X)$ defined in the interval [0,1], what can be the minimum value of its expectation ${E} (X)$?

Answer 1

When $p$ increases, that means its cumulative distribution function

$$P(x) = \int_0^x p(x)\,\mathrm{d}x$$

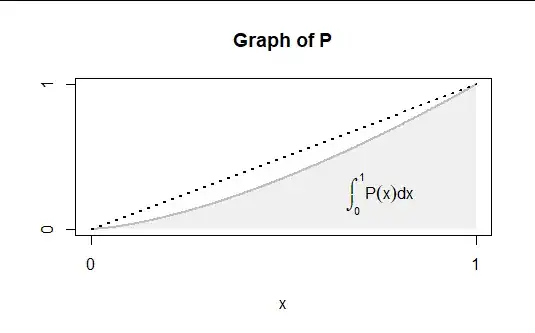
is convex. Since $P(0)=0$ and $P(1)=1,$ the convexity implies the graph of $P$ lies on or below the line segment connecting $(0,0)$ and $(1,1),$ a segment that covers a triangular area of $1/2.$ (The graph is the graph curve and the segment is the dotted line in the figure.) Thus, the area under the graph of $P$ cannot exceed $1/2:$

$$\frac{1}{2} \ge \int_0^1 P(x)\,\mathrm{d}x.$$

This area is that of the shaded region in the figure:

Since $$E_p(X) = \int_0^1 (1-P(x))\,\mathrm{d}x = 1 - \int_0^1 P(x)\,\mathrm{d}x \ge 1 - \frac{1}{2},$$ it follows that $E_p(X) \ge 1/2.$ This minimum value is the best possible because it can be attained by the uniform distribution where $p(x)=1$ for $0\le x \le 1.$

Answer 2

First, change the problem to say that the density is non-decreasing and piecewise constant. Solve that problem first and then return to this problem.

Suppose there is a density $f(x)$ that minimizes $EX$ where $n$ is a positive integer and for the integers $1 \le i \le n$ the density is constant and equal to $a_i$ on each of the the intervals $((i-1)/n,i/n)$. The constants are non-decreasing and $a_1 \le a_2 \le ... \le a_n$. If there is any $j$ where the inequality is strict $a_j<a_{j+1}$, then you could define a new density equal to $f(x)$ outside of the interval $((j-1)/n,(j+1)/n)$ but constant and equal to the average $\frac{a_j+a_{j+1}}{2}$ in the interval $((j-1)/n,(j+1)/n)$ and then $EX$ would be strictly smaller. Thus, all $a_i$ must be equal to $1/n$. The uniform density has that property and is the only density that has that property for all $n$. If X is uniform, $EX=\frac{1}{2}$.

That proof only works for piecewise constant densities, but for an arbitrary density, the integral is defined as the limit of these piecewise constant approximations. Thus, the minimum over arbitrary non-decreasing densities is also $\frac{1}2$.

For the original problem, where you want $f(x)$ to be increasing, for any small $\epsilon>0$, you can have $EX=\frac{1}{2}+\epsilon$ by taking $f(X)=1+6\epsilon(2 x-1)$. But you can never have $EX=\frac{1}{2}$ with an increasing density because of the argument above.