Visualizing shared instances of p-values

Question

Assume a data table that presents the p-values of a large number of independent runs of a statistical hypothesis test. Each run represents a single test with two possible hypotheses (i.e., null and alternative) on a particular dataset (or treatment or whatever you want to call it). A total of d different datasets (represented in the table as rows) and h different hypotheses (represented as columns) were evaluated to generate the table. The data table, thus, portrays the p-values of d x h different runs.

     |   h1    h2    h3    h4
----------------------------
d001 | 0.02* 0.33  0.01* 0.46
d002 | 0.14  0.25  0.03* 0.11
d003 | 0.01* 0.68  0.01* 0.04*
...
d998 | 0.02* 0.71  0.01* 0.13
d999 | 0.03* 0.29  0.02* 0.33

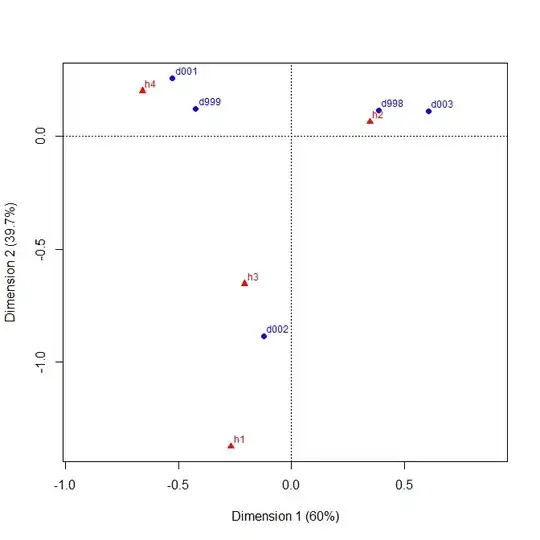
Since the number of datasets evaluated ranges in the hundreds, I would like to find a way to visualize shared instances of significance graphically. Specifically, I would like to highlight if any of the hypotheses (i.e., columns) share instances of p-values<alpha with other such hypotheses for the same datasets (i.e., rows). In the above example, hypotheses h1 and h3 share instances of p-values<alpha across numerous datasets.

What general type of visualization would you recommend? (I'll set up the R code myself and am just interested in the type of visualization that you would recommend.)

Answer 1

Ultimately, you want a biplot. Briefly, a biplot rerepresents your units / rows as points in a 2-dimensional space that maximizes the amount of the original variability that can be captured. (These are the first two principal components; for more, see: Making sense of principal component analysis, eigenvectors & eigenvalues.) It likewise rerepresents your variables / columns as the tips of arrows in the same space on the scatterplot. In general, the closer two points are, the more similar they are; the closer the tips of two arrows are, the more similar the variables are; and the closer a point is to a variable, the larger the proportion of its mass is associated with the variable, and vice-versa. Be aware that a high-dimensional space is being collapsed into 2-dimensions, so there will be some error there, but that's the gist of it. There is a lot of good information about biplots available on the site, click the tag, sort by votes and start reading from the top to learn more.

I strongly believe it is best to use the full information in data and not dichotomize (e.g., into significant vs. non-significant). Here is a biplot of your example dataset of p-values, coded in R:

d = read.table(text="dataset    h1    h2    h3    h4
                        d001  0.02  0.33  0.01  0.46
                     ...
                        d999  0.03  0.29  0.02  0.33", header=T)
rownames(d) = d$dataset
d           = d[,-1]
d
#        h1   h2   h3   h4
# d001 0.02 0.33 0.01 0.46
# d002 0.14 0.25 0.03 0.11
# d003 0.01 0.68 0.01 0.04
# d998 0.02 0.71 0.01 0.13
# d999 0.03 0.29 0.02 0.33

windows()
  biplot(prcomp(d, scale=T))

We can see that h1 is similar to h3, d003 is similar to d998 in pattern, and that d998 has most of its mass in h2.

If you really want to know only about significance, you can conduct a correspondence analysis. That also outputs a biplot, although by convention usually with points for both rows and columns, and the table is decomposed using a different metric than correlations (which PCA uses). We also have several good threads on correspondence-analysis.

d2           = as.data.frame(sapply(d, function(j){  as.numeric(j<.05)  }))
rownames(d2) = rownames(d)
#      h1 h2 h3 h4
# d001  1  0  1  0
# d002  0  0  1  0
# d003  1  0  1  1
# d998  1  0  1  0
# d999  1  0  1  0
library(ca)
windows()
  plot(ca(d))

We get generally similar information here.