4

I was under the impression that if I randomly sample from a skewed normal distribution, the distribution of my sample would be normal based on central limit theorem, but the graph clearly shows that it's not the case.

Can someone help me understand where I'm wrong in my assumptions?

import random
import numpy as np
from scipy.stats import skewnorm
import matplotlib.pyplot as plt


skewed = skewnorm(4)
sample = skewed.rvs(100000)

sampled = []
[sampled.append(random.sample(set(sample), 1)[0]) for _ in range(100)]

fig, ax = plt.subplots(1, 1)

ax.hist(sampled)
plt.show()

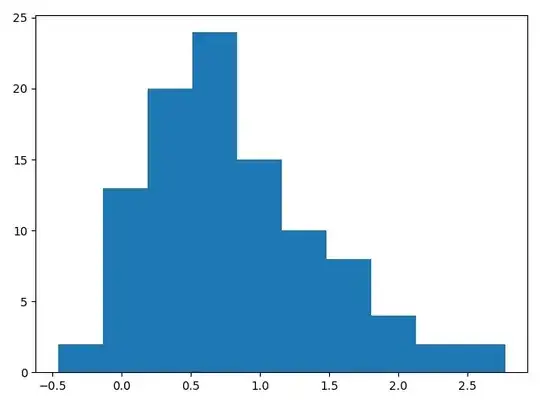
enter image description here

mdewey
  • 16,541
  • 22
  • 30
  • 57
Mehdi Zare
  • 197
  • 9
  • 5
    Please see this question of mine from last year: https://stats.stackexchange.com/q/473455/247274. You’re making the same mistake about the CLT that most everyone makes for a while. – Dave Feb 15 '21 at 22:40
  • 4
    Instead of your complicated and **incorrect** way involving list comprehension to obtain `sampled` (incorrect because you may e.g. obtain as a "sample" only the first element 100 times), you may simply write `sampled = random.sample(sample, 100)` – MarianD Feb 16 '21 at 00:32
  • Maybe the terminology here is confusing? I can understand that some people would expect a *skew normal distribution* to be normal, just as a *long beard* is also a beard, a heteroskedastic regression is still a regression, ... – kjetil b halvorsen Mar 05 '22 at 15:20

2 Answers2

12

I was under the impression that if I randomly sample from a skewed normal distribution, the distribution of my sample would be normal based on central limit theorem

You are incorrect in your understanding of the central limit theorem (it is a pretty common misconception, as Dave pointed out). The CLT states that under certain conditions the limiting distribution of the sample mean is normal, not that data sampled from a non-normal population will have a normal distribution.

You can see this in action if you run a different simulation, where you simulate the sample means:

import random
import numpy as np
from scipy.stats import skewnorm, norm
import seaborn as sns
import matplotlib.pyplot as plt


skewed = skewnorm(4)

simulated_means = []

for i in range(10000):
  data = skewed.rvs(100)
  simulated_means.append(np.mean(data))

sns.distplot(simulated_means, fit=norm)
plt.show()

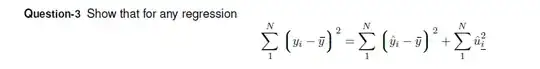
Sampling distribution of the mean

In this particular case, we see that the sample distribution of the mean is more or less normal when n=100; the normal fit is the black line. This will not always be true, since the CLT is an asymptotic result, but simulations like this help us understand how the sampling distribution from a particular population with a particular sample size might look.

Louis Cialdella
  • 1,404
  • 12
  • 17
1

By analogy:

Let's assume there is a country whose population of 10 million people consists of 1 man and 9,999,999 women.

Do you expect that by increasing the size of the sample you will be more and more close to the “normal” ratio 1:1 (1 man for 1 woman)?

Other argument – for your skewed distribution:

If you take as a sample the whole population (i.e. the very very large “sample”), then by some miracle your skewed population suddenly changed to a normal one?

MarianD
  • 1,493
  • 2
  • 8
  • 17
  • 3
    I don't think the first analogy is useful: by "normal" the OP is referring to the Normal (Gaussian) distribution, not "normal" in the sense of what one would normally expect. You could alter the answer to talk about heights (which do follow a roughly Gaussian distribution) and it would be more useful. – JDL Feb 16 '21 at 09:13
  • @JDL, analogy is just an analogy, isn't it? – MarianD Feb 16 '21 at 09:41
  • 1
    it isn't actually analogous though (your second argument is fine, it's just the first one I find unhelpful) – JDL Feb 16 '21 at 09:46
  • 1
    @JDL, I respect your opinion even though the mine is different. – MarianD Feb 16 '21 at 11:12