Linear regression prediction intervals not increasing when extrapolating beyond training set

Question

If I'm using a model in a predictive capacity it would be useful to have a quick way of seeing whether I'm applying it outside of the data space it was trained in, and thus I should take care with the results. However, I've observed that prediction intervals (PIs) don't really increase enough to act as a warning system. Is there a general statistical way of doing this, or should I just implement a warning system specific to my application?

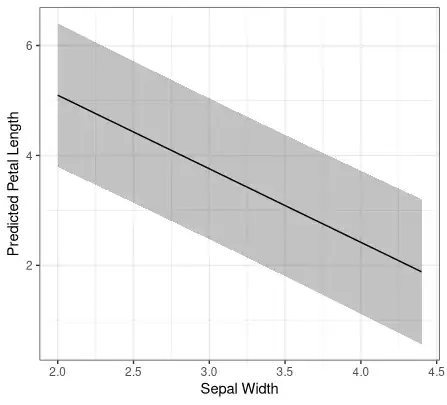
To illustrate the point, a model of petal length from sepal length and width gives a nice nearly constant width PI for an average sepal length and width covering the full range of the training data.

library(tidyverse)

mod <- lm(Petal.Length ~ Sepal.Length + Sepal.Width, data=iris)

new_sepal_width <- seq(2, 4.4, length.out=100)
preds <- predict(mod, data.frame(Sepal.Length=5.8, Sepal.Width=new_sepal_width), interval='prediction')
as.data.frame(preds) %>%
  mutate(sepal_width = new_sepal_width) %>%
  ggplot(aes(x=sepal_width)) +
    geom_ribbon(aes(ymin=lwr, ymax=upr), alpha=0.3) +
    geom_line(aes(y=fit)) +
    labs(x="Sepal Width", y="Predicted Petal Length", title="Sepal length = sample mean of 5.8 and sepal width covering full sample range") +
    theme_bw()

If I now hold the sepal length constant at double the maximum observed training set value, and allow sepal width to increase up tot double the max training set value, the PI isn't noticeably wider (the blue line is the maximum training set sepal width). I also tried the bootstrapped PIs from this answer but they were almost identical to the analytical solution.

new_sepal_width <- seq(2, 8.8, length.out=100)
newdata_extrapolate <- data.frame(Sepal.Length=16, Sepal.Width=new_sepal_width)
preds <- predict(mod, newdata_extrapolate, interval='prediction')
as.data.frame(preds) %>%
  mutate(sepal_width = new_sepal_width) %>%
  ggplot(aes(x=sepal_width)) +
    geom_ribbon(aes(ymin=lwr, ymax=upr), alpha=0.3) +
    geom_line(aes(y=fit)) +
    geom_vline(xintercept = 4.4, colour='blue') +
    labs(x="Sepal Width", y="Predicted Petal Length", title="Sepal length = double sample max (16), sepal width goes up to double sample maximum (8.8)") +
    theme_bw()

score 2 · Accepted Answer · answered Feb 10 '21 at 00:12

The width of the prediction interval is probably not the best way of acting as a "warning sign". If you have tons of data, the estimates will be very precise and hence the prediction interval will be relatively constant even when you extrapolate far beyond the original data. See the example below. The training data has 95% of its observations between -1 and 1, and yet the prediction interval only increases about 2%. That is a very small change for such an absurd extrapolation.


x = rnorm(10000, 0, 0.5)
y = 2*x + 1 + rnorm(10000, 0, 0.3)
mod = lm(y~x)
#extrapolate to x=10
preds <- predict(mod, list(x = seq(-1,10,length.out = 100)), interval='prediction')

as.data.frame(preds) %>%
  mutate(x = seq(-1,10,length.out = 100) ) %>% 
  ggplot(aes(x=x, y = fit)) +
  geom_ribbon(aes(ymin=lwr, ymax=upr), alpha=0.3) +
  geom_line(aes(y=fit)) +
  labs(x="Sepal Width", y="Predicted Petal Length", title="Sepal length = sample mean of 5.8 and sepal width covering full sample range") +
  theme_bw()

A better way may be to come up with some rule based on the quantiles of the training data. For instance, when using a natural spline, we force the spline to be linear when the predictor is in the upper 2%-5% based on the number of knots and size of the data. I don't think there are definitive rules for such a "warning signal" as applications will vary. You might want to try and devise of such a rule yourself.

That's a good point about the sample size too, as that's also an issue I'm facing in my application. I'll tailor something to my use case then, thanks — Stuart Lacy, Feb 10 '21 at 11:50

Linear regression prediction intervals not increasing when extrapolating beyond training set

1 Answers1