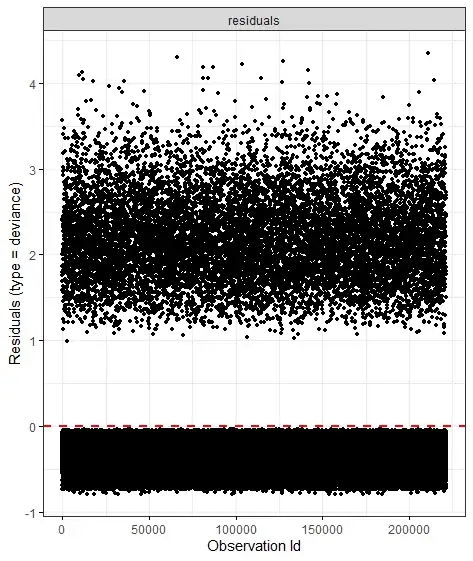
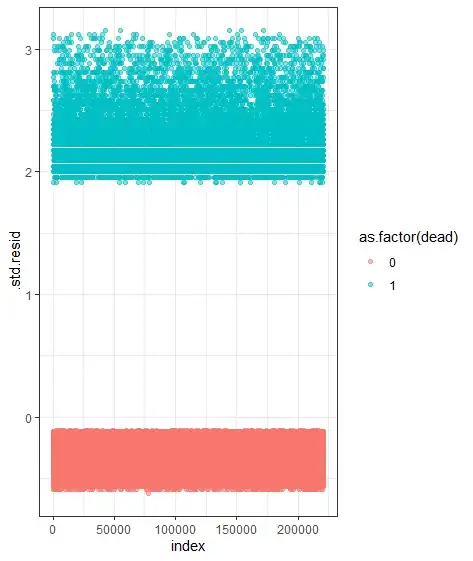
For the Cox model deviance residuals, see this page for discussion. Censored cases necessarily have negative deviance residuals; they don't have observed event times, so their event times can't be earlier than predicted (the requirement for a positive deviance residual). Deviance residuals can be helpful in identifying outliers, but your data don't suggest any massive outliers. There are many other things that you need to check to validate your model. On the other hand, one might expect some event cases to have negative deviance residuals, so you need to look into the data in more detail. I wonder whether censoring might be informative in your data set, which would lead to problems with a simple Cox analysis.
For the logistic regression I'm not sure what's going on, although informative censoring could be playing a role here too. In general I'm skeptical of logistic regression when the underlying issue is a time-to-event problem, except for situations when there is essentially complete follow up beyond the time of interest. My guess is that there was a good deal of censoring before the time point chosen for logistic regression on your data.
In response to comments:
A similar pattern of residuals appear even if I have only a single predictor or/and if the predictor is something as straight-forward as age (so death ~ age). With the original coding, the model statistics are 0.085348 (coef), 1.089096 (exp(coef)), and 0.003834 (SE); in the reversed coding, they are 0.0465651 (coef), 1.0476663 (exp(coef)), and 0.0005984 (SE).
The "reversed coding" switches censoring with event indicators, and can provide information about whether there might be information included in the censoring. Note that the magnitude of the coefficient for age in the "reversed coding" is almost half as large as the age coefficient in the standard age/survival model. That is, your age variable predicts censoring about half as well as it predicts events, leading to questions about whether the censoring itself might be informative, as increased age is associated with both earlier events and earlier censoring. Cox models assume that censoring is uninformative.
You should certainly examine the distributions along the time axis of the events and the censorings, e.g. with histograms or density plots. You don't want your censorings to tend to happen earlier than your events.
Furthermore, the standard error of the age coefficient in the "reversed coding" is substantially smaller than that in the standard age/survival model, suggesting that you have many fewer events than you have censored cases: maybe 20 times or so more censored cases than events. A large excess of censored cases, all of which necessarily have negative deviance residuals while the mean deviance residual is 0 by construction, could be partly to blame. In the extreme situation with only 1 event and other cases censored, the case with the event will necessarily have a positive deviance residual, occurring at an earlier time than the model predicts. How many events you would have to add to have at least one event case with a negative deviance residual is hard for me to judge.
Given that your variables predict both censoring and events, your model probably at least needs appropriate case weighting to take the distribution of censoring times into account. Otherwise your results will be biased in terms of application to an underlying uncensored population. See Hernán and Robins, particularly Chapter 8 on selection bias and chapter 17 on survival modeling.
Another thing to consider is whether you are omitting important survival-associated predictors from your model. As in logistic regression, omitting such predictors in a Cox survival model tends to bias regression coefficient estimates downward in magnitude toward 0. A downward-biased coefficient for age in your survival model would thus over-estimate survival and tend to lead to positive deviance residuals for cases with events (events happening earlier than predicted by the model). Again, how big a role this omitted-variable bias plays here depends on your data.