1

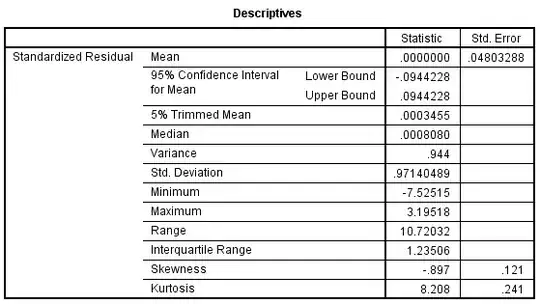
Is it necessary to transform the data here in order to stabilize the variation in this series? I do not think it is.

How "bad" do the fluctuations have to be before stabilization becomes necessary?

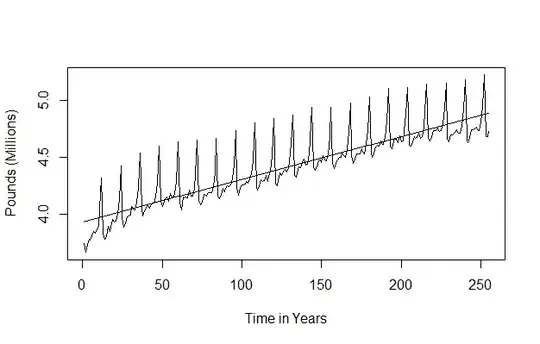
enter image description here

I'm assuming a linear trend is suitable; not concerned with the seasonal effects. However, I am concerned that the trend line is a bit low.

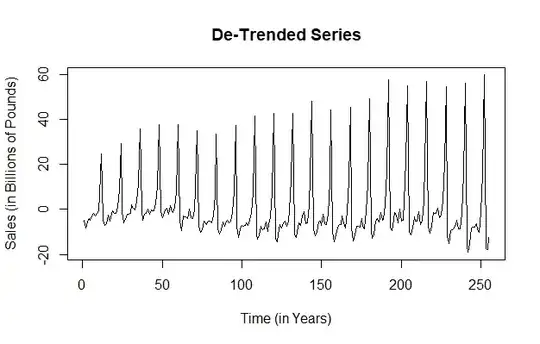
enter image description here

I've detrended the series, but the variance seems to not be stabilized here at all.

enter image description here

I obtain the following plot after transforming the data with the $\ln$ transformation. However, I do not see how it is different compared to my first plot.

enter image description here

Detrending the transformed data does seem to make the variance more stable. Has transforming the data helped in this case?

enter image description here

Chesso
  • 313
  • 1
  • 6

1 Answers1

1

I believe the best answer for your question is: it depends on what you are trying to achieve.

If your intention is to present a smoothed version of this time series, then the answer would be yes. You could apply some kind of "noise filter" to smoothen the series, so your plot would look more like a linear trend. But if you intend to fit a model over the data you could use an approach that takes seasonality and trend into account.

As an example, your model could look like this:

$ log(y_t) = b_0 t + b_1 s_{t-n} + \alpha_0 + \alpha_1 log(y_{t-1}) + \alpha_2 log(y_{t-2}) + \epsilon_t$.

Where $t$ would be the trend component and $s_{t-n}$ the seasonality component. In this case, the answer would be no, because you would deal with seasonality and trend somehow.

rodrigocfaria
  • 136
  • 4
  • 1
    And just eyeballing the data, I reckon things might be scaling multiplicativly (i.e. replacing $y_t$ with $\log(y_t)$ might work better). (The clue is the size of the seasonal fluctuations scaling up with the annual value). – Stephen McAteer Feb 07 '21 at 23:34
  • 1
    @StephenMcAteer It really makes sense. Updating my answer to use $log(y_t)$ instead of $y_t$. Thank you :) – rodrigocfaria Feb 07 '21 at 23:50