Context
My question is related to the binmedian algorithm which is suggested in this post and its implementation originally in C and its adaptation in python.
My issue with these algorithms is that they are not truly online in the way they are implemented: the only thing they do is compute the median in one pass given the full array $X = \left[ x_1\; x_2\;\dots\;x_{n-1}\;x_n\right]$. They claim the memory footprint is $O(1)$ but they still require the full array $X$ as input.
Question
Assume at step $k$ you only know two things: the step number $k$, the value $x_k$ and the estimator at the previous step $\theta_{k-1}$. This happens when $X$ has very large memory footprint (say $n>10^7$) and one only wants to load $X$ in batches of small sizes (here assume batch of size $1$).
What would be a good recurrence relation to get $\theta_k$ from $k$, $x_k$ and $\theta_{k-1}$ ? I do not mind storing auxiliary variables as long as they have a (small) fixed size that does not depend on $n$.
Related posts
The following posts answer the question quite well:
The livestats python package is very close to what I want, but when experimenting with gaussian mixtures I've had strange behaviors.
Experiments
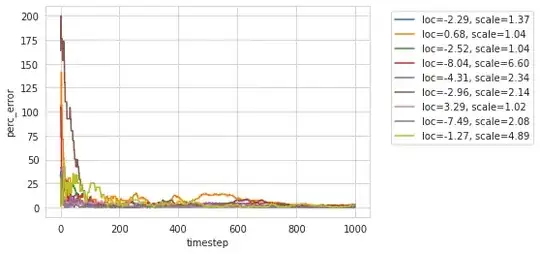
When plotting the relative error percentage of the estimated median $\theta_k$ to the target $t_k$ $$ \mathrm{perr}(\theta_k, t_k) = 100\cdot\dfrac{\lvert t_k - \theta_k\rvert}{\lvert t_k\rvert}$$ where $t_k$ is computed using the full array $\texttt{np.median}(X)$, I find important variability in the first $10^3$ samples,
But the relative error stays below $5\%$ after $10^3$ samples
I'll open another question if I encounter problems in my experiments.