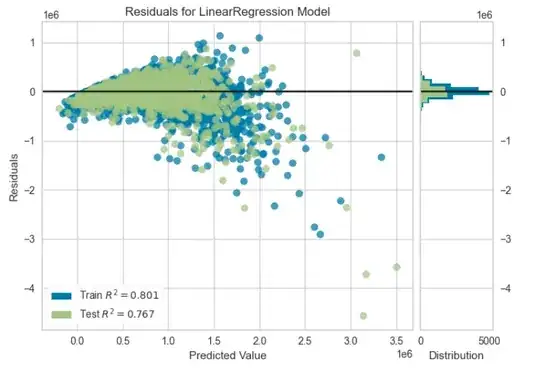
I have a problem understanding the residual plot from yellowbrick.
I have created the following plots:
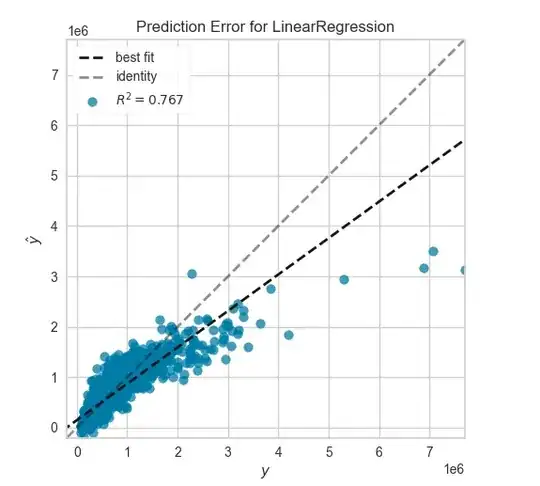
If I take a look at the first one: It shows the predicted value on the $y$-axis and the real value on the $x$-axis. That means in this case, that some of my predicted values are too low, correct?
If I now take a look at the residual plot: As far as I know the residuals value is calculated with: $\text{residual} = y_\text{real} - y_\text{predicted}$
This would mean that a negative residual value would express that some of my predicted values are too high, correct?
How can this correlate? This seems to be the inversed message compared to the first plot? What is wrong in this case? Do I have to invert the residuals calculation?
Thank you in advance Lukas