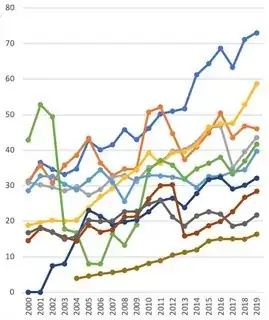
I have a data set of the revenues of 10 different large companies from the years 2000 through 2019. Here they are all plotted in one graph. The y-axis has a unit of billions of Euros:
What I found interesting about this, is that the company with the brown revenue plot seems to have a very stable growth pattern. (This is the line with the least revenues in 2019; it consistently appears at the bottom from 2004 onwards.) In other words, the discrete function that maps the years to their corresponding revenues seems to be the least "rough" for the company with the brown colour.
We can formalize this idea of roughness by defining it as follows: for a vector $x$ containing the y-coordinates of the time series, the roughness $R$ is defined as
R = sd(diff(x))/abs(mean(diff(x))).
Here, sd denotes the standard deviation, diff comprises the vector of differences of the consecutive values of $x$, abs is the absolute value and the mean is the average.
Question: are there any statistical tests that allow one to compare the roughness of discrete functions with one another, and to conclude that one (set of) function(s) is indeed less or more rough than another (set of) function(s) ?