Comparing fits of linear models that use different data spans of a curve (and why does AIC seem to work)

Question

Several related questions have been asked.

This one is similar, but it does not match this question exactly.

Also, i seem to have results that contradict the accepted answer there.

Data

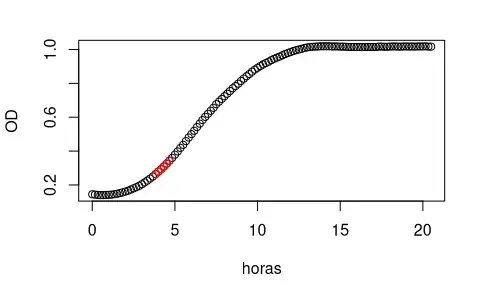
An imperfect growth curve (a time series).

Goal

Briefly, we take our not-quite-sigmoid growth curve, and try to find a linear region of maximum width and slope.

Ideally, we need a method that identifies regions that "significantly" fit a straight line (including zero-slope regions), and choose the one that has the maximum slope (and width).

Approach so far

Without a "score" for linear goodness-of-fit, we used sliding windows of size of 6 to scan the first and second derivatives of the data. The size 6 was chosen arbitrarily, seeing that our data was roughly linear in that time scale.

For the maximum slope region, we looked for the window with a maximum in the first derivative (which also coincided with a zero crossing in the second derivative, i.e. an inflection point).

For maximizing the width of the linear region (not sacrificing goodness-of-fit) we tried several approaches, and the best was the following:

1. Take the initial 6-point window (defined previously by max in dx/dt), fit a linear model to it, and compute AIC.
2. Extend the window to the right, by including the next observation along with previous data, and recompute the linear model and it's AIC.
3. Repeat previous step until no more points are left in the series.

Method notes

• The AIC was calculated with R's AIC(), giving it lm(log2OD ~ horas) as input.
• We only extended the initial window to the right just for simplicity. How the window should "grow" seems to be a matter for another question.
• Since the points are always separated by 10 minutes, index is equivalent to horas in the plots.

Results

By this method, the window of size 6 with maximum slope is highligted in red in the following plot:

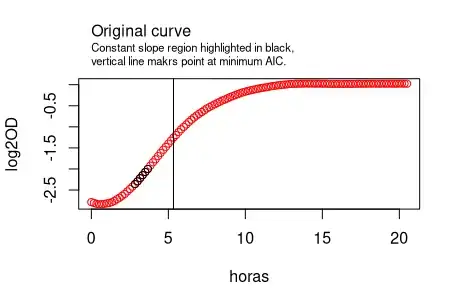
Next, we observed that the AIC value decreases as more points are added (by extending the window to the right), but only up to a point and then increases again. That AIC minimum is marked by a vertical black line.

In the following plot we show that the minimum AIC window corresponds to the time just before a transition between the exponential growth phase (linear at the middle), and the stationary phase (the plateau to the right).

Thoughts

I have read that AIC is used "only" to compare maximum-likelihood models with the same data. However it seems useful in this case. Explanations on why it may [not] be wrong to use it like this are welcome.

The answer posted here contradicts the results shown above.

I have also tried using: R2, Ljung-Box test, Durbin-Watson test, among others. But none of them have shown the rather useful behavior of the AIC. The former are monotone, and the latter has that interesting minimum.

Questions

1. What is the best way to find linear regions in a curve? I have searched for alternatives and came across piece-wise linear models, or the "Chow test", though I am not familiar with them (nor with AIC really).
2. Is there an appropriate goodness-of-fit way of finding linear regions of maximum span? (i.e. comparing models using different but overlapping spans of the time series).
3. Why is there a minimum in AIC? According to a previous answer it's value should always increase when adding more points.

Thanks!