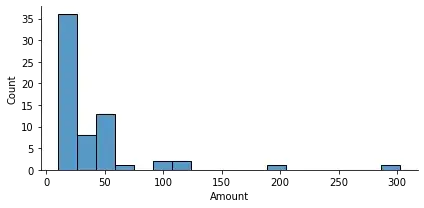
I am trying to calculate the 95% confidence interval of the mean value of the population. I have this data:
[ 23.0, 70.0, 50.0, 53.0, 13.0, 33.0, 15.0, 40.0, 23.2, 19.0, 33.0,
110.0, 13.0, 45.0, 53.0, 110.0, 53.0, 13.0, 10.0, 30.0, 13.0, 50.0,
15.0, 20.0, 53.0, 15.0, 10.0, 10.0, 13.0, 13.0, 100.0, 13.0, 13.0,
43.0, 30.0, 25.0, 18.0, 23.0, 23.0, 23.0, 13.0, 203.0, 30.0, 23.0,
23.0, 43.0, 30.0, 53.0, 23.0, 13.0, 10.0, 20.0, 33.0, 13.0, 23.0,
23.0, 12.0, 303.0, 55.0, 53.0, 23.0, 103.0, 45.0, 13.0 ]
The distribution of which looks like this:
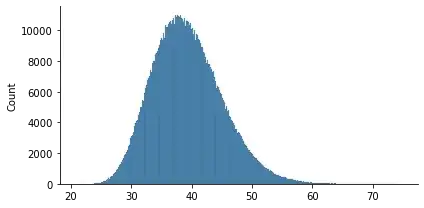
I tried to bootstrap resample this with 62 observations per sample but the means do not form a normal distribution. I thought with the central limit theorem the means would converge on a normal distribution the number of samples grew. But even with 1,000,000 samples the distribution is skewed right:
means = []
# resample 1,000,000 times
for i in range(100000):
mean = resample(s).mean()
means.append(mean)
Which gives me the following distribution of means:
ShapiroResult(statistic=0.9881454706192017, pvalue=0.0)
Indicates that we should reject the null hypothesis that the samples are drawn from a normal distribution.
Is there an assumption for the central limit theorem that I am missing? Why doesn't the means of these samples form a normal distribution?
I've read several posts on the central limit theorem and the bootstrap method but most deal with what should happen, not cases where it doesn't work.