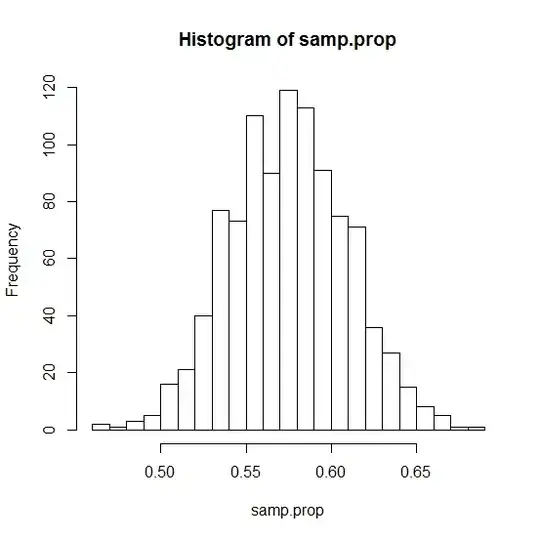
Suppose the registrar's office at a college reports 58% of the students live on campus. An intern working in the administration building is unaware of this 58% parameter value. He designs a study in which he will take a random sample of 200 students and estimate the population proportion of all students that live in the college dorms using the resulting sample proportion.
If he were to repeat his study many times, the possible values of the sample proportion would vary by about __ away from the expected value of __, on average.
I understand the first blank is the standard deviation and the second is the mean, but why can't I approximate them using $\mathcal{N}(np, (np(1-p))^.5)$, which is the normal approximation to a binomial distribution? So that I have $\mathcal{N}(116, 6.98)$? So the first blank is 6.98 and the second is 116?