2

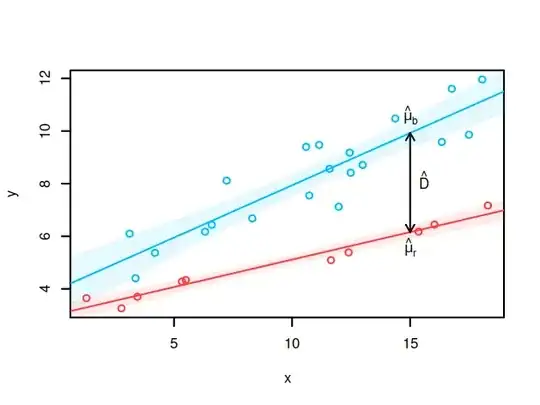
Assume two linear regression models

$$ Y_{b} = \beta_{0b} + x\beta_{1b} + \varepsilon_b \qquad \text{with} \qquad \varepsilon_b \sim N(0, \sigma_b^2) \\ Y_{r} = \beta_{0r} + x\beta_{1r} + \varepsilon_r \qquad \text{with} \qquad \varepsilon_r \sim N(0, \sigma_r^2) $$

and the residual errors are independent ($\varepsilon_b \bot \varepsilon_r$).

My goal is to calculate an exact confidence interval (CI) for the difference between the fitted values of the two models at a specific $x$.

enter image description here

This could be easily done if the two regression lines have about the same residual standard error (see here or here).

Question: How can I get a CI for the difference if $\sigma_b^2 \neq \sigma_r^2$?

Approach: I guess this is like generalizing Welch's $t$-test to the regression framework. However, I am not sure if this is correct?

$$ \frac{\hat{\mu}_b - \hat{\mu}_r - (\mu_b - \mu_r)}{\sqrt{\frac{s^2_{\hat{\mu}_b}}{n_b-1} + \frac{s^2_{\hat{\mu}_r}}{n_r-1}}} \sim t_\nu $$

And how do I get the degrees of freedom $\nu$?

I guess some bootstrap approach might also work but I am more interested in a classical test statistic.

retodomax
  • 91
  • 1
  • 6
  • Shall we presume all $\varepsilon_b$ are independent of the $\varepsilon_r$? – whuber Jan 14 '21 at 15:38
  • 1
    @whuber Yes, this can be assumed – retodomax Jan 14 '21 at 15:38
  • Given independence, fit the regression model with all the data. Include an interaction between group and X. Express the differences you want in terms of the parameters of that interaction model, and have the software compute the correct standard errors. – BigBendRegion Jan 14 '21 at 16:17
  • @BigBendRegion That does not explain my question: How to allow for different residual standard errors? Is my pivot correct? What is the correct degrees of freedom for the $t$-distribution? – retodomax Jan 14 '21 at 16:23
  • Either model it or use robust standard errors. – BigBendRegion Jan 14 '21 at 16:29

0 Answers0