I read these two threads:
Why are principal component scores uncorrelated?
and learned that PC modes are by definition orthogonal and thus uncorrelated. So why do I see people plot PC modes against each other if they're uncorrelated? In what case will e.g. a PC1 vs PC2 plot reveal a meaningful correlation?
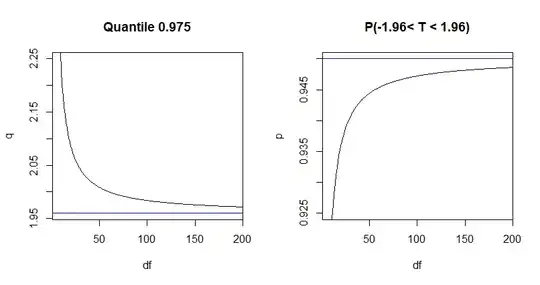
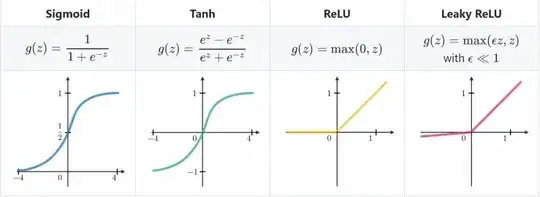
It's true that PCs are orthogonal, implying zero Pearson correlation and no linear relationship between them. However, zero Pearson correlation doesn't generally imply independence. The PCs might be nonlinearly related, reflecting nonlinear structure in the data. For example, consider the 3d 'swiss roll' dataset below (left). Its projection onto the first two PCs (right) shows the spiral structure.
Furthermore, even if the PCs turn out to be independent (which we wouldn't know a priori), plotting them can still reveal something useful about how the data are distributed. For example, consider the clustered 3d dataset below (left). Its projection onto the first two PCs (right) shows the clustered structure.
PCA scatterplots are just low-dimensional visualizations of the data. One use is to learn something about the structure of the underlying distribution. This won't always work; e.g. sometimes the underlying structure can't be adequately captured by low dimensional linear projections. But, it's often a good first-pass attempt. Another use is to visualize how the data are related to some external variable, e.g. by coloring points in the scatterplot according to the variable of interest.
