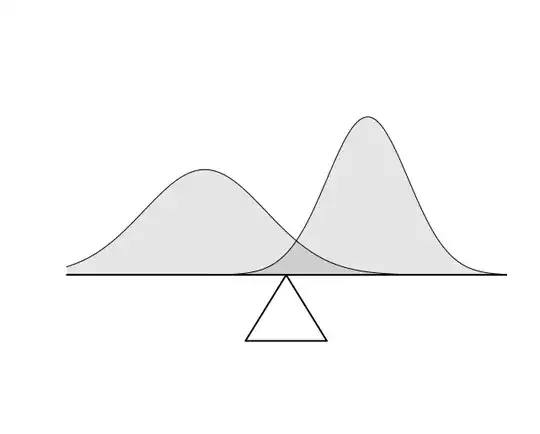
Seeking the expected value of a continuous random variable we calculate the integral $\int_{-\infty}^\infty xf_X(x)\ dx$.
Does the integrand $xf_X(x)$, i.e. the product of $x$ and the corresponding density, have any (interesting) interpretation?
(An analogous question could be posed for the case of a discrete random variable.)