I am working on modeling the electricity output of a single power plant.
More specifically, I am trying to compute causal effects of a variable prop on output. My model would look something like this
$$ output = \beta_0 + \beta_1 prob + \boldsymbol{d}'\boldsymbol{X} + u $$ where I omit the time index $t$ for brevity. The covariate vector $X$ can include lags of the dependent variable.
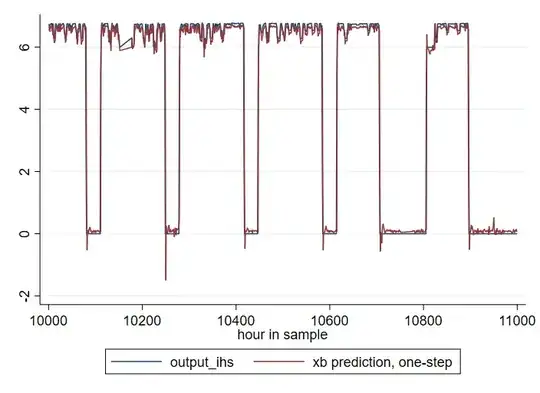
The problem I have is that the dependent variable seems like it could be an intermittent time series, which would render a classic modeling approach unsuitable. The periods with subsequent zeros are different in duration they do not follow each other in a constant frequency.
Consider the figure below, where the blue line represents the original data and the red line the predicted values of a model that includes nine lagged terms of the dependent variable. It is quite obvious that the ARX model I chose does not consider the zero-bound, which would render my estimate of $\beta_1$ unreliable.
I have read about approaches like Croston's method or INARMA. However, they seem to focus completely on forecasting, which is not the goal here. How can I estimate the model such that it follows the true data generating process and estimates a reliable value for the parameter of interest?
The variables were transformed using the inverse hyperbolic sine transformation in order to smooth the variance. This explains the units of measurement.
Many thanks in advance!