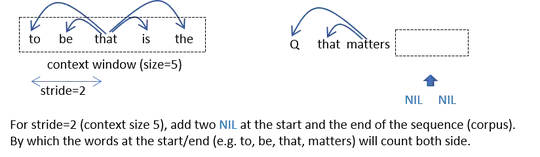Background
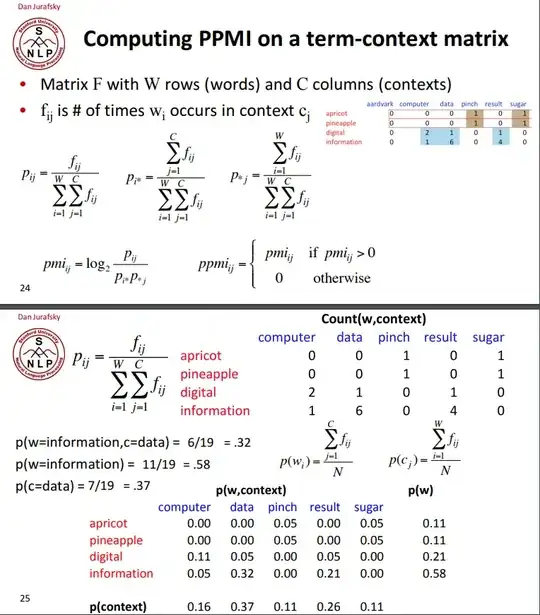
When calculate PMI or PPMI from a co-occurrence matrix (COM), it sums each row (co-occurrences) of the COM e.g. 2 for pineapple as in the formula in the snapshot. For this question, it is about words co-occurrences in a corpus text sequence.
Question
Can the PMI formula calculate correct PMI from a COM? I think this part in the formula does not give the number of co-occurred words for the row i.
$\sum_{j=1}^Cf_{ij}$
Example
Creating a COM from text sequence using N-Gram(N=5).
Each word between or and Q has four co-occurrence words (COW), e.g. (to, be, is, the) for the word that. However, the word matters at the end only has two COW (Q, that).
Therefore, $\sum_{j=1}^Cf_{ij}$ for each words are:
- 6 for to (i = 1) --> cannot calculate from dividing by COW
- 7 for be (i = 2) --> cannot calculate from dividing by COW
- 4 for or (i = 3) -->
or occurred (4 / COW) times = 1 - 4 for not (i = 4) -->
not occurred (4 / COW) times = 1 - 7 for that (i ==5) --> cannot calculate from dividing by COW
- 4 for is (i = 6) -->
is occurred (4 / COW) times = 1 - 4 for the (i = 7) -->
the occurred (4 / COW) times = 1 - 4 for Q (i = 8) -->
Q occurred (4 / COW) times = 1 - 2 for matter (i = 9) --> cannot calculate from dividing by COW
For those words at the ends of the corpus, $\sum_{j=1}^Cf_{ij}$ does not represents how many times the word at row i occurred.
Workadound
By padding both ends of the corpus with NIL, the number of times when a word occured can be calculated via $\sum_{j=1}^Cf_{ij} / COW$ at each row i. However, a COM will not include such dummy NIL word counts.
Then the formula to calculate PMI/PPMI seems not to be completely accurate regarding those words at ends, although it could be negligible when the corpus size or vocabulary size is big.
Please help to clarify the accuracy of PMI, or if I misunderstand COM such as COM is different from my understanding and there is no such issue.