It's obviously a translation, but logically correct. P-value is probability, under $H_0$, of a more extreme result of the test statistic in the direction(s) of the alternative hypothesis than the observed value of the test statistic. [For a two-sided alternative, two probabilities are added to get the P-value.]
Consider the following normal samples (from R) and a Welch 2-sample t test to see
whether their sample means are significantly different; specifically to test
$H_0: \mu_1 = \mu_2$ against $H_a: \mu_1 < \mu_2.$
set.seed(1234)
x1 = rnorm(20, 100, 10)
x2 = rnorm(25, 110, 12)
Welch Two Sample t-test
data: x1 and x2
t = -2.0301, df = 40.54, p-value = 0.02447
alternative hypothesis:
true difference in means is less than 0
95 percent confidence interval:
-Inf -1.046619
sample estimates:
mean of x mean of y
97.49336 103.62038
Under $H_0,$ the test statistic is approximately distributed as Student's t
distribution with 41 degrees of freedom. So one would reject $H_0$ at the
5% level if $T \le -1.683.$
qt(.05, 41)
[1] -1.682878
However, the $T = -2.0301$ is even smaller than this 'critical value'. The P=value
is the probability $P(T \le -2.0301) \approx 0.0244,$ computed under $H_0.$
pt(-2.0301, 41)
[1] 0.0244342
In the figure below the P-value is the area under the density curve to the left of the vertical red line.
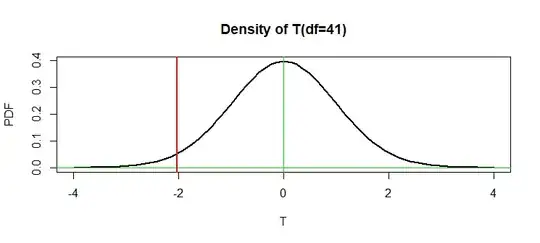
By contrast, if this were a two-sided test $H_0: \mu_1=\mu_2$ against $H_a: \mu_1 \ne \mu_2,$ then the P-value would be
$P(|T| \ge 2.0301) \approx 2(0.244) = 0.0488.$ So the sample means differ significantly at the 5% level of significance.
t.test(x1, x2)
Welch Two Sample t-test
data: x1 and x2
t = -2.0301, df = 40.54, p-value = 0.04894
alternative hypothesis:
true difference in means is not equal to 0
95 percent confidence interval:
-12.22426952 -0.02977364
sample estimates:
mean of x mean of y
97.49336 103.62038
In the figure below the P-value is the sum of the areas outside
the vertical red lines.
Note: If this were a pooled two-sample t test, then the degrees of freedom for the t statistic under $H_0$ would be $\nu = n_1+n_2 - 2 = 43.$ Because this is a Welch t test and sample variances are
not exactly equal, the degrees of freedom are computed according to a formula that involves $n_1, n_2, S_1^2,$ and $S_2^2.$ giving
$\min(n_1-1,n_2-1) \le \nu \le n_1+n_2-2.$
For the current data, $\nu = 40.54.$ R shows fractional degrees of freedom; printed tables of t distributions and some software program use only integer degrees of freedom.

