-2

Is a P value of 0.4 statistically significant for a Wilcoxon Rank Sum test?

Jamerson2
  • 97
  • 1
  • 1
    In order to be significant at the 5% level, the test should have P-value smaller than 0.05. // So P-value of 0.4 is not significant at any level usually considered of practical use. – BruceET Jan 04 '21 at 08:04

1 Answers1

1

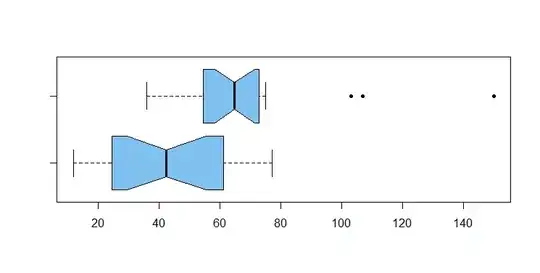
Here is an example with data sampled (in R) from distributions of the same shape, but with a rightward shift of $12$ for the second sample.

set.seed(121)
x1 = rgamma(20, 5, .1)
x2 = rgamma(20, 5, .1) + 12

The two sample medians happen to differ by about $22.5.$

summary(x1)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  12.10   24.62   42.50   43.53   61.02   77.18 
summary(x2)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  36.05   55.61   64.94   68.40   72.53  150.03

Roughly speaking, the fact that the 'notches' in the sides of boxes in the boxplots do not overlap is taken as an indication that the two samples are not from the same distribution.

boxplot(x1, x2, notch=T, horizontal=T, col="skyblue2", pch=20)

enter image description here

The Wilcoxon signed-rank test has P-value $0.0014 < 0.05$ so the two sample medians are significantly different at the 5% level (also, for this particular example, at the 1% level).

wilcox.test(x1, x2)

        Wilcoxon rank sum test

data:  x1 and x2
W = 85, p-value = 0.001435
alternative hypothesis: 
  true location shift is not equal to 0
BruceET
  • 47,896
  • 2
  • 28
  • 76