Takeuchi’s information criterion is said to be the generalization of AIC to misspecified models. That publication presents DEGREES OF FREEDOM FOR NONLINEAR LEAST SQUARES ESTIMATION. From that source:
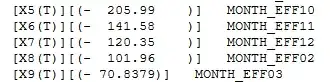
This appears similar to a Tikhonov regularization. Would someone please explain what Takeuchi’s information criterion is in simple language? It would appear that calulating degrees of freedom is not simple. In addition to df calculations, are there other uses for TIC? If, as George Box says "Essentially, all models are wrong...." which application of AIC is not to misspecified models? Should we all be using TIC as opposed to AIC?