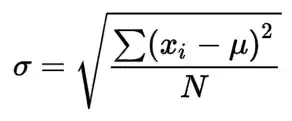Is it really appropriate to say "standard deviation" is variation or dispersion

Question

Question

I have been struggling to convince myself that SD (standard deviation) is about variation or dispersion.

Standard deviation From Wikipedia, the free encyclopedia

In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values.

Is it really an appropriate claim to say average distance from the mean is measure of variation or dispersion? It can be, with specific data sets, but is it really appropriate to say so in general?

As stated in Is standard deviation a proper measure of dispersion of data ?, it seems claiming SD as measure for variation or dispersion could be questionable without cautions in what situations it can be.

Standard deviation has become the most widely used measure of dispersion of data. A measure of dispersion can, in the true sense, be regarded as the proper measure of dispersion if the measure is based on the deviations between all pairs of data.

Standard deviation is, however, not based on the deviations between all pairs of data. Accordingly, the perfectness of standard deviation, as measure of dispersion, is questionable. Therefore, the question is " Is standard deviation a proper measure of dispersion of data ? "

I have not been able to understand how is standard deviation, which is not based on the deviations between all pairs of data, a proper measure of dispersion? The explanation is not as clear as to convince that standard deviation, is a proper measure of dispersion.

Is using the word standard appropriate as well? I suppose if each distance is divided by SD, it could be said as standardized, but what is SD itself is standardizing?

If I follow this Standardization explanation:

In statistics, standardization is the process of putting different variables on the same scale. This process allows you to compare scores between different types of variables.

If there are two data sets X and Y, and SD always makes X and Y comparable on the same meaningful scale/unit, then I believe it is. But is it so?

References

• Why is it called the “standard” deviation?

Pearson made up this term in 1894 paper "On the dissection of asymmetrical frequency-curves", here's the pdf.

• What is a standard deviation?

Answer 1

I'm not aware of any widely understood set of formal criteria that a purported measure of dispersion has to meet^†—perhaps it's more that dispersion is a vague, pre-quantitative, notion that has motivated & can apply to various precisely defined measures. The assertion that "a measure of dispersion can, in the true sense, be regarded as the proper measure of dispersion if the measure is based on the deviations between all pairs of data" is intriguing; but its author doesn't provide any rationale (or any reference).^‡ This criterion would not in fact rule out the standard deviation: for a sample ${x_1, \ldots, x_n}$, the sum of squared deviations from the mean is equal to the mean of squared pairwise differences,

$$\sum_{i=1}^n{\left(x_i- \frac{\sum_{i =1}^n x_i}{n}\right)^2} = \frac{\sum_{i=1}^n\sum_{j = i + 1}^n(x_i - x_j)^2}{n}$$

(see @whuber's answer to "Why isn't variance defined as the difference between every value following each other?").

---

† @NickCox made me aware in short order that Bickel & Lehmann (1976), propose such a set of criteria. A measure of dispersion must (1) be location-invariant, (2) be scale-equivariant, & (3), given distributions $F_X$ symmetric about $\mu_X$ & $F_Y$ symmetric about $\mu_Y$ where $|X-\mu_X|$ stochastically dominates $|Y-\mu_Y|$, be greater (or at least equal) for $F_X$ than for $F_Y$.

That's quite intuitive, but to propound criteria for a measure of dispersion for an asymmetric distribution, you'd have to privilege one particular measure of central tendency—conjuring the spectre of mean-dispersion, median-dispersion, &c. Bickel & Lehmann (1979) take a different tack: noting that for symmetric distributions $X$ is more dispersed than $Y$ when

$$ \begin{align} F_X^{-1}(v) - F_X^{-1}\left(\frac{1}{2}\right) &\leq F_Y^{-1}(v) - F_Y^{-1}\left(\frac{1}{2}\right)\quad \forall\, v \leq \frac{1}{2}\\ F_X^{-1}(v) - F_X^{-1}\left(\frac{1}{2}\right) &\geq F_Y^{-1}(v) - F_Y^{-1}\left(\frac{1}{2}\right)\quad \forall\, v \geq \frac{1}{2} \end{align} $$

, they decide that for asymmetric distributions $X$ is more spread out than Y when

$$ F_X^{-1}(v) - F_X^{-1}(u) \geq F_Y^{-1}(v) - F_Y^{-1}(u)\quad \forall\, u < v $$ So any two quantiles of $X$ are farther apart than the corresponding quantiles of $Y$; the same probability mass is spread more thinly.

See the papers for proofs that standard deviation is both a measure of dispersion (for symmetric distributions) & of spread (for both symmetric & asymmetric distributions).

---

‡ I see the rationale now: it's equivalent to saying that a dispersion measure must be invariant to translation (& to reflection if the deviation is unsigned). From the set of pairwise distances you can reconstruct the original sample (or finite population) $(x_1, \ldots, x_n)$ only with unknown location & orientation: $\pm(x_{(1)}+k, \ldots, x_{(n)} + k)$.

---

References:

Bickel & Lehmann (1976), Ann. Statist., 4, 6, "Descriptive statistics for nonparametric models. III. Dispersion".

Bickel & Lehmann (1979), in Contributions to Statistics: Jaroslav Hajek Memorial Volume, "Descriptive statistics for nonparametric models, IV. Spread".