0

Disclaimer: I already asked this question once, however it was misunderstood and I was told by a moderator to repost it: Random number (between 0 & 1; > 5 decimal places) from binomial/beta-like distribution, with set mean (same as mode & median) and set variance

First of all this question is very similar to others linked just below. However, none of the answers I saw are correct/precise enough for a distribution with the same mean, mode and median.

Distribution that has a range from 0 to 1 and with peak between them? & Beta-distribution: how to generate a peak at certain mean value with a control on variance in extrems

What I need is a random number generator that draws from a distribution like the distributions below, for which I can set the mean and variance.

What I want the distributions to look like for a few example cases: enter image description here Notice that at 0.5 it should be like a truncated normal distribution and if the mean is smaller or bigger than 0.5 it should be a skewed distribution. And I want to be able to specify the variance and make it narrower or broader without it affecting the skewness/shape.

What I need it for: I am working on a stochastical model, which calculates the fraction of plant biomass eaten over whole plot which is made up of 100 cells. I then want to remove that fraction of plant biomass in each gridcell. However, I want to have some randomness in it so that it takes more from one gridcell and less from another etc. Thus I need to draw a random number based on the fraction and at the start of the model I want to specify the variance of the random fractions. I also want the fraction that I input to be the most likely number to be drawn (i.e. the mean is supposed to be the same as the mode).

Here are the rules the random number X needs to follow:

Conditions that X itself has to fulfill:

  1. X must be between 0 to 1 (including 0 and 1).
  2. X must have at least 5 decimal places (ideally unlimited, but 5 would be enough maybe even 4)

Conditions that the distribution from which X is drawn hast to fulfill

  1. The mean is also the mode (or at least better than with a beta distribution).
  2. The distribution should look like a binomial/beta distribution. So that it is skewed if the mean is above or below 0.5 (see first picture).

Input that I give:

  1. The mean can be any number between 0 and 1. At most I would want to round it to 4 digits but ideally I want it to be unchanged when I give it to the random number generator.
  2. I want to be able to set the variance freely, but relative to the mean (e.g. if mean is 0.6 variance should be 0.04 but if mean is 0.99 variance should be much smaller than 0.04). I want to set this variance once at the start.

Approaches I have tried and why they failed:

I have not managed to get either binomial distributions or beta distributions to work. I haven't found anything else. Here are the problems with either distributions. Maybe it will give you ideas. If you are interested in the code check my previous question: Random number (between 0 & 1; > 5 decimal places) from binomial/beta-like distribution, with set mean (same as mode & median) and set variance.

Problem with the binomial distribution:

It is not continuous i.e. I cannot set the variance independently from the number of decimal places the random number will have. E.g. if I want to have high variance I can do that by reducing the amount of events I simulate in the binomial distribution. For example only 6, however that means that I reduce my possible numbers to (0,0.2,0.4,0.6,0.8,1). If I increase the events then I get more decimal places; however the distrbution will be extremely narrow around the mean and look normally distributed.

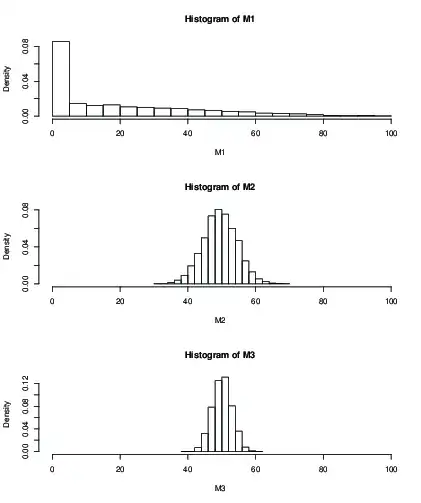Histogram with events = 5, n =100,000, mean 0.8. Good variance, but numbers dont have enough decimal places Histogram with events = 5, n =100,000, mean 0.8. Has the variance I would want, but I cannot draw any numbers inbetween.

Problem with beta distribution:

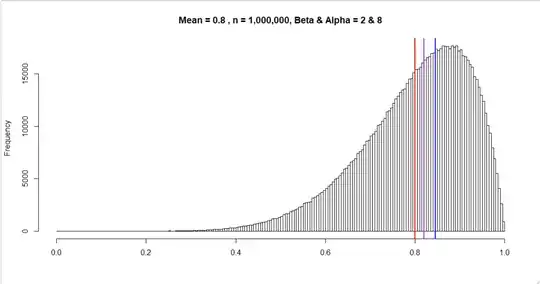
The beta distribution allows me to keep variance the same (relative to the Mean) but change the mean freely. I have accomplished this by keeping beta always at a certain number and varying alpha, based on the mean. But the mean (red) does not coincide with the mode/maximum (blue) (nor median (purple)).

Beta distribution

Do you have any ideas on how to draw a number from a distribution with a shape like the binomial one (see second picture) and with the same mean and mode, but with more decimal places. Is this even possible? I just need random numbers from that distribution, it doesnt need to be continous, I dont mind if it is just an approximation or if it is constructed from two distributions or if it's a workaround. I am writing a stochastical model so small differences from mean and mode would not be problematic as long there is no bias. I will be implementing this random number generator in C++ but answers in other languages are also fine like e.g. R.

Before you answer please double-check that your answer would consider my rules for the random number I specified above.

Alex
  • 25
  • 4
  • For the distribution that is not symmetric it might be hard to have mean = mode. It is not impossible, but in most cases lack of symmetry would lead to mean, mode and median not being equal. Are you sure that what you expect to see is a reasonable assumption? – Tim Dec 17 '20 at 21:53
  • 1
    @Tim It's easy to make the mean, median, and mode coincide by using a suitable mixture of the right and left tails. But we're really discussing mathematical juggling of distributions: there just isn't enough information presented in either question to supply a good *statistical* proposal for a family of such distributions. – whuber Dec 17 '20 at 22:03
  • As long as the mean is of my distribution corresponds to the fraction eaten over the whole plot it would reasonable. It would just be one kind of variability. E.g. with the binomial distribution it worked, however the removal of biomass for each cell was very limited cause the variance I needed meant that only 0.05, 0.1, 0.15 ...1 could be removed. – Alex Dec 17 '20 at 22:05
  • @whuber I know it is possible and not that hard, just asking if the assumption is reasonable. The shapes of the distributions used as examples do not look like ones that would easily fit this constraint. – Tim Dec 17 '20 at 22:08
  • @whuber What information are you missing? – Alex Dec 17 '20 at 22:23
  • I have found it's much more powerful and interesting to use models that bear some cognizable relation to the subject being studied. Often, a quantitative theory, statistical principles, and/or previous data will suggest a good model. In your case the criteria you impose appear artificial and have no evident connection with the subject matter. – whuber Dec 17 '20 at 22:25
  • @whuber I want to know if the variability that biomass is being removed has an effect on the plant growth on the plot overall. If I find out that different distribution result in differing plant growth, it might be worth considering for a future field study to look at the distribution with which it is being removed. If I find out that regardless of distribution the result is the same such a field study might not be worth it and I know I do not need to consider it. If I dont have the tools to compare differing distributions I will never know, so why not give me the tools and let me decide. – Alex Dec 17 '20 at 22:42
  • 1
    Your account suggests that some of your restrictive criteria are inessential. What would be the matter with using a suitable Beta distribution, for instance? Why would the mode matter? – whuber Dec 18 '20 at 13:08
  • @whuber Why would it not matter? I do not know! If you go to the extreme and either take all or nothing (according to the mean) I am sure that would have an impact on the plant growth. That's why I want to find out, see my previous comment. If it is possible and easy as you have suggested before, why don't you just show me how!? – Alex Dec 18 '20 at 15:43
  • 2
    As in your previous q., wanting >5 decimal places seems at best an odd way to specify that your variable is continuous. Number of decimal places is a presentation choice; it's not an inherent mathematical property. Your condition that mean $=$ mode even if the variable is skew strikes me also as artificial and implausible. Can you show data close to those shapes? It's possibly achievable by splicing together left and right tails but, sadly or otherwise, you're not tempting anyone to try the messy mathematics. I would start with a beta distribution and consider powering it. – Nick Cox Dec 19 '20 at 02:29

0 Answers0