tl;dr
This looks cool, relates possible to discrete regression, but I don't know the term for what it is to do this.
I want to learn more. It looks interesting and useful. Can you point me to references or content in this area?
Background:
My daughter made cookies for her science project. I helped her with the math part, but she wanted to optimize the a recipe.
I told her that she would want to avoid the "evil" of "one factor at a time" (link) because it misses interactions, in inefficient with data, and gives more erroneous answers. A simple designed experiment can do a better job with fewer tests.
She did research and determined that two reasonably well studied "axes" she could look at are savory vs. sweet. She did not want to look at "pumpkin nut habanero" cookies.
Initially we were looking at a $3^2$ design on a savory vs. sweet axis, but it presents some serious challenges. It is a ton of cookies to make. There are 9 distinct recipes and it is hard to rank-order them. Doing ordinal regression to find an optimum isn't trivial. We could reduce the number of tests to 5 and make a basic design and get somewhere. Instead of rank-ordering, we could do paired comparison and while it is more taste testing, it is easy to believe that a person can nearly always pick which they think is better.
Here is the what the 2-axis 5-test design looked like.
When top-down is implausible I think of bottom up. I used a random forest and made an estimator that swept the domain and answered the paired tests with the one that was closest.
Here is how it discretized the domain.
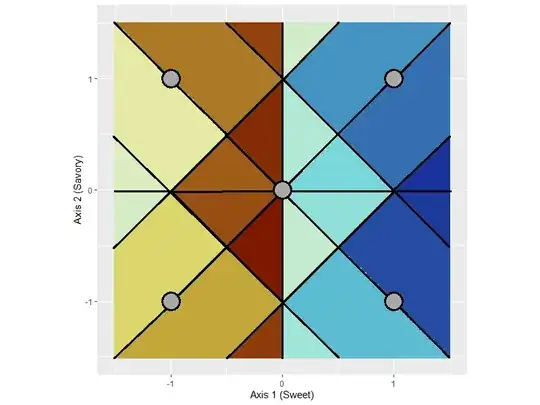
It seems both convenient and clever that 10 tests can reduce the area where "best lives" by a factor of 24. Personally I don't like to extrapolate, so I would bound to a square going from (-1,-1) to (1,1) which makes only 16 sub-divisions.
Question: What is the name of the technique here? Someone has to have done something like this before. Who was it, what did they do, and where do I read up on it?
I don't know if the paired testing still counts as discrete choice. I've seen JMP that called "choice designs" but in contrast this approach allows discovery of a parcel that isn't in one of the test elements.
There is a very elegant simple way, so simple a 6th grader can do it, to derive the way the "landscape" gets sliced up based on the point locations.
This has to have been invented before, but I have no idea what the process is called, so I don't know how to look it up in the literature.