Why is the intercept different from the mean of Y when X=0?

Question

I was hoping to find here a solution to some aspects of linear regression I had trouble understanding.

Let's take an example of regression with the following variables:

• $y:\:$ depression (continuous)

• $x:\:$ time (treated as continuous and coded as following:

  • 0=timepoint 1;
  • 1=TP 2;
  • 2=TP 3;
  • 3=TP 4;
  • 4=TP 5)

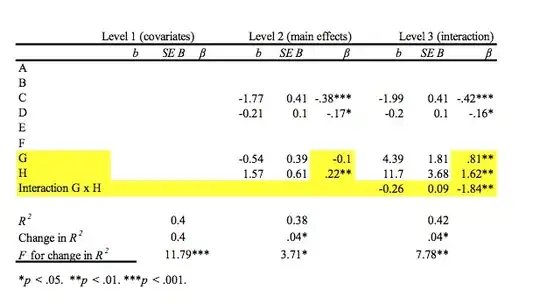
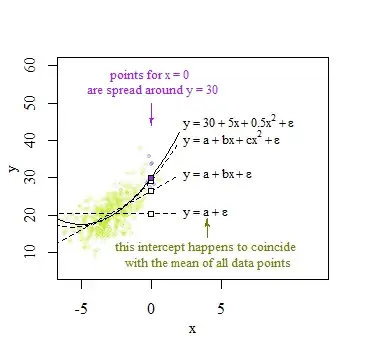
Everywhere I look, the definition for the intercept goes something like this: the intercept is the expected mean value of y when x=0. As I understand, in this case the intercept should be the mean for depression when time=0. However, these seems not to be the case. When a calculate the mean for timepoint 1 I get 39.65, but the intercept is 39.91 (see below).

As I already stated, for me "mean value of y when x=0" is the same as saying "mean value of depression at timepoint 1 (coded as 0)", so it doesn't make sense to me why the two values differ.

I also want to mention:

• When I have only 2 timepoint in variable Time, the intercept is the same as the mean
• When i treat time as a factor, the intercept is the same as the mean
• I've checked with other variables and datasets too

mean(subset(data, Time==0)$depression) 

    [1] 39.65254

m0 <- lm("depression~Time", data=data)

summary(m0)

    Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
    (Intercept)  39.9158     0.7156  55.781  < 2e-16 ***
    Time         -1.6381     0.3029  -5.408 1.05e-07 ***

Answer 1

In OLS regression the intercept (and slope also) is estimated using all the observed data, not just observed data where $x=0$, specifically $\widehat{\beta}_0 = \overline{y} - \widehat{\beta}_1\overline{x}$. This estimate of the intercept should therefore not be expected to equal to the observed $\overline{y}|x=0$ which is calculated using only observed values where $x=0$.

If it helps, you can think of $\overline{y}|x=0$ as a biased estimator of the intercept (if all OLS assumptions are true, naturally).

PS I hope my combining bar and hat symbols in my explanation is not too jarring. :)

Answer 2

This is a graphical representation of @Alexis's answer - hope it helps.

Here, since the mean of the three groups of Time points do not quite align on a straight line, the intercept of the linear fit does no match the mean of depression at Time 0 (red bar is the mean of depression at Time = 0).

set.seed(123)
dat <- data.frame(
    Time= rep(c(0, 1, 2), each= 10),
    depression= c(rnorm(n= 10, mean= 0), rnorm(n= 10, mean= 4), rnorm(n= 10, mean= 5))
)

mean_at_0 <- mean(dat[dat$Time == 0,]$depression)
fit <- lm(data= dat, depression ~ Time)

plot(dat$Time, dat$depression)
points(x= 0, y= mean_at_0, pch= '-', col= 'red', cex= 4)
abline(a= fit$coefficients[1], b= fit$coefficients[2], col= 'blue')


fit$coefficients[1]
(Intercept) 
        0.7 

mean_at_0
[1] 0.075

Answer 3

I think you're confusing population parameters with parameters estimated from the sample. If you have a linear model $Y=a+bX+\epsilon$, the intercept $a$ is $a=E[Y|X=0]$. This means that the intercept coincides with the population mean conditioned to $X=0$, but the estimated intercept (using ordinary least squares, for example) does not need to coincide with the sample mean of data with $X=0$. In fact, there may not be any sample point with $X=0$) at all!

So the way to understand the intercept is as follows: if you draw a large number of samples $(X,Y)$ with $X=0$ from the same population from where you draw your sample, and you take the mean of $Y$ over those points, in the limit when the number of samples goes to infinity you get the intercept.

Answer 4

Some related questions are

• Why do my (coefficients, standard errors & CIs, p-values & significance) change when I add a term to my regression model?
• Why is the intercept in multiple regression changing when including/excluding regressors?
• Why and how does adding an interaction term affects the confidence interval of a main effect?

Some images related to those answers are.

I will skip the detailed descriptions of these images and hope that they can speak for themselves without descriptions (in the linked questions you can see more detailed information).

But, I hope that you can see in these images that the same data is fitted by different curves which have different values at the intercept. So the 'intercept' is ambiguous and can mean different things which do not need to be equal

• the mean of the sampled data at $x=0$
• the mean of the population at $x=0$
• the (estimated) mean of the model at $x=0$

Especially when the model is biased then the estimated intercept does not need to coincide with the data points (which you see in several curves in the images above), and sometimes the intercept might be even meaningless (which you see in the data about the cars, 2nd image above).