0

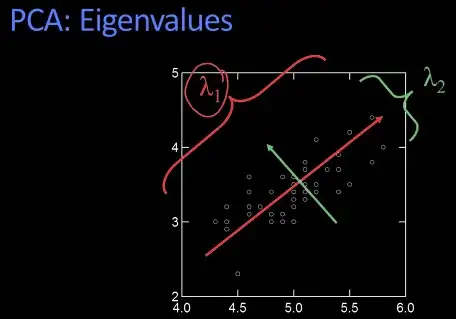
In this video, it is said that:

The axis of least inertia [is the axis] of greatest variance.

However, this link says the axis of least inertia is also the axis of least variance, which makes sense to me. So is the video incorrect? What am I missing here?

display name
  • 33
  • 5
  • What does the lecturer and/or you mean 'least inertia'? We can factor the covariance matrix and order the vectors (potentially not uniquely if one eigenvalue occurs more than once) according to the absolute values of the eigenvalues... what is the inertia then? – Fabian Werner Dec 10 '20 at 15:57
  • The book that is quoted in the link says the same as the video. It is only said that it could reportedly be the opposite but no source is given. – manu190466 Dec 10 '20 at 21:36

1 Answers1

1

I think this is the answer:

The confusion comes from the use of axes. For the same axis, the amount of variance (sum of distance from point to axis) is the same as the inertia.

However, the video refers to the variance about the red axis ($\lambda_1$, the principal eigenvector) and the inertia about the green axis, which explains the statement in question.

img1

display name
  • 33
  • 5