How to group countries with similar age distributions?

Question

How can I group the world's 200-odd countries into (say) ten groups, with each group's countries having 'similar' age distributions?

I want to compare COVID-19 fatality rates across countries. But the proportion of aged is a confounding variable. I don't have the age-breakup of COVID fatalities for every country. Instead, I have population counts for each age group (e.g., "Country X has 10.3 million in the 10 to 20 age group", and so on).

So basically I want to stratify countries and compare within the resulting groups. Intuitively, 'older' countries like the US and Greece would be in different groups from 'younger' ones like India or Mexico. How would I go about this using R or another language?

A commenter asked why I didn't standardize fatality rates against some reference age distribution. That's because I suspect information on differences inherent to these countries may be lost in such standardization process.

Specifically, I'm comparing Covid-19 mortality with flu vaccination rates of the aged and there's a correlation (1) -- but I have to account for differences in national age distributions. I don't have age information on for Covid deaths in each country. So stratification is the only other approach I can think of.

Source data: https://sourceforge.net/p/costat/code/ci/master/tree/

Answer 1

Why not standardizing the data?

You write

That's because I suspect information on differences inherent to these countries *may be lost in such standardization process.

and you write

but I have to account for differences in national age distributions.

I find this contradictory because age standardization is a way to account for differences in national age distributions.

But, you also write

I don't have age information on for Covid deaths in each country.

That is a valid reason why you can not use age standardization. You simply lack the information to do it.

Use a hypothetical age distribution

You could apply a hypothetical age distribution of deaths for the countries where you do not have this information.

You can do this by computing for all countries where you have the age information the relative risk of fatality as a function of age and based on that compute the hypothetical age distribution of the fatalities (hypothetical: if the distribution of fatalities would be according to the estimated/observed risk ratio in each age category)

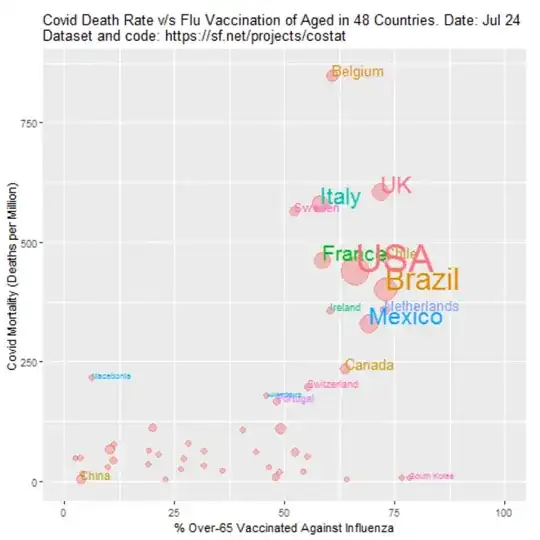
Below is an example from the code below. The comparison is made with the death rates in the Netherlands. The x-axis gives the expected death rate in a country if it would experience the same age-dependent death rates as observed in the Netherlands. For instance you see Japan (JPN) with an old population having a high expected death rate and China (CHN) with a young population having a low expected death rate. On the y-axis you see the actual observed death rates. For this data and this set of countries, there is no clear correlation or dependency between age and death rate (this means that while age plays a role, it are other factors that are much more important in determining the death rate in a country).

Scale factor dependent on age distribution

Effectively this standardization based on a hypothetical age distribution provides a scale factor by which you multiply the fatality rate. You mention that information might get lost in this way. What you could do instead is perform a regression not on the transformed variable but by using the scale factor as an additional parameter in the model. You can do this either by making the classification into ten groups, but you could also use this scale factor without discretizing and as a non-categorical variable.

Simpler way

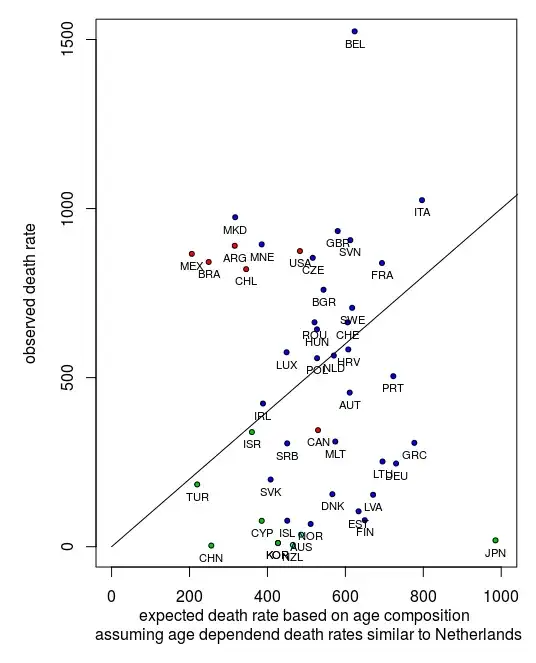
The above might be too complex and depending on the public that you are using your analysis for it might be difficult to explain your data and get you into (possibly unneccesary) details. An alternative is that you just use the % of the population that is 65 or older (or use some other age cutoff).

In the image below you see how the complex factor computed with the code below, is not much different from the percentage of the population older than 65.

Example code and graph

Eventually, the difference due to the standardization is not so big (the difference with your image is due to the data in this graph being from December instead of August). This is because many other factors play a more important role than age.

In addition, the effect of the parameters that you are investigating, influence vaccination, is not so clear. Even if the effect would be clear then there are too many other factors involved and you can not really say that influenza vaccination has a causal effect (I guess that this might be what you attempt to show).

library(countrycode)
library(readxl)


### data files
data  <- read_excel("Downloads/data.xlsx", sheet = "main")

### XLSX from UN https://population.un.org/wpp/Download/Standard/Population/
data2 <- read_excel("Downloads/WPP2019_POP_F07_1_POPULATION_BY_AGE_BOTH_SEXES.xlsx", skip = 16)

### CSV from RIVM https://www.rivm.nl/coronavirus-covid-19/grafieken
#data3 <- read.csv("~/Downloads/leeftijd-en-geslacht-overledenen.csv", sep=";")
#agecases <- rowSums(data3[,2:3]) ### adding male + female columns
agecases <- c(0,   0,   0,    2,    0,    3,    6,
              13,  11,  42,   76,   133,  241,
              474, 942, 1538, 2063, 2283, 1414, 534)

### John Hopkins data
data4 <- read.csv("https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv")




### selection of countries which have flu vaccination data
sel <- which(!is.na(data$flu))
sel <- sel[-6] ### Remove Liechtenstein for lack of age distribution data
datasel <- data[sel,]


### get a reference key to connect rows with same countries from the two data sets
years <- data2$`Reference date (as of 1 July)`
countries <- countrycode(data2$`Country code`, origin = 'iso3n', destination = 'iso3c' )
refkey <- sapply(datasel$ccode, FUN = function(x) {
                    which((years == 2020) * (countries == x) == 1)[1] 
                })
refkey <- as.numeric(refkey)

### get covid cases from JH data
cc <- 'USA'
name <- countrycode(cc, origin = 'iso3c', destination = 'country.name')

ncases <- function(cc) {
  subsel <- c(1)
  
  ### special cases where JH data has multiple regions
  if (cc == 'NLD') {subsel <- c(5)} ### only use Netherlands, no colonees
  if (cc == 'DNK') {subsel <- c(3)} ### only use Danmark, no Greenland + Faroe  
  if (cc == 'GBR') {subsel <- c(11)} ### only use UK, no colonies 
  if (cc == 'FRA') {subsel <- c(11)} ### only use France, no colonies  
  if (cc == 'AUS') {subsel <- c(1:8)} ### sum all provinces  
  if (cc == 'CAN') {subsel <- c(1:16)} ### sum all provinces  
  if (cc == 'CHN') {subsel <- c(1:33)} ### sum all provinces  

  name <- countrycode(cc, origin = 'iso3c', destination = 'country.name')
  
  ### special cases where JH data uses other country name
  if (cc == 'USA') {name <- 'US'}
  if (cc == 'KOR') {name <- 'Korea, South'}
  
  rows <- which(data4$Country.Region == name)[subsel]
  nc <- max(colSums(data4[rows,-c(1:4)])) ### get the last non-empty column (which is the maximum)
  
  return(nc)
}
ncases <- Vectorize(ncases)

# compute age dependent risk (incidence) based on Netherlands
# this will be roughly an exponential function of age
nrow  = refkey[27]
data_row <- data2[nrow,]
agepop <- as.numeric(data_row[9:28])*1000
agepop[20] <- agepop[20] + as.numeric(data_row[29])*1000  ## combine 95-99 and 100+ to create 95+
agerisk <- agecases/(agepop/10^6)  ### cases per million


###
### function to compute risk based on age distribution
### this will give the risk if the death rates 
### would be according to the data of the Dutch RIVM
###
age_risk <- function (nrow) {
  data_row <- data2[nrow,]
  agepop <- as.numeric(data_row[9:28])*1000
  agepop[20] <- agepop[20] + as.numeric(data_row[29])*1000  ## combine 95-99 and 100+ to create 95+
  avgrisk <- sum(agerisk*agepop)/sum(agepop)
  return(avgrisk)  
}
age_risk <- Vectorize(age_risk)
risk <- age_risk(refkey)  


### plotting

deaths <- ncases(datasel$ccode) ### deaths per country
pop <- datasel$pop



### color + size of bubbles
region <-  countrycode(datasel$ccode, origin = 'iso3c', destination = 'continent' )
color <- as.numeric(as.factor(region))+1
size <- 1+sqrt(datasel$pop)/10^4

### scatterplot
plot(datasel$flu, (deaths/(pop/10^6))/risk, log = "y", 
     pc = 21,
     col = 1, bg = color, cex = size, xlim = c(0,100),
     ylab = "standardized incidence \n (1 = equal to Dutch RIVM figures)",
     xlab = "influenza vacination rates"
     )

lines(c(-10,110),c(1,1), lty = 2, col = 8)

### add labels
text(datasel$flu, (deaths/(pop/10^6))/risk, datasel$ccode, cex = 0.7, pos = 4)