0

When sample size $n$ gets large, we know that a sorted set of the $n$ samples approaches the inverse cumulative distribution function (CDF) sampled at $\frac{1}{n}, \frac{2}{n}, \dots, \frac{n}{n}$.

enter image description here

But when we reduce $n$ to smaller sample sizes, as shown in the figures below, convergence to the inverse CDF is extremely poor.

Are there bias tricks, sampling or estimation techniques, or modifications to the CDF (i.e. a different weighting scheme than $\frac{1}{n}, \frac{2}{n}, \dots, \frac{n}{n}$), that allows us to work confidently with small sample sizes? How can we improve the convergence of a small sample size to the inverse CDF?

enter image description here

enter image description here

Python code:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

for n in [1000, 100, 20]:
    plt.figure()
    plt.title("sample size={}".format(n))
    plt.plot(norm.ppf(np.linspace(0, 1, n)), label="invcdf")
    plt.plot(np.sort(np.random.normal(size=n)), label="sortsample")
    plt.legend()
    plt.show()
develarist
  • 3,009
  • 8
  • 31
  • 4
    Poor only by the unrealistic standards of expecting a small sample to be a miniature of its parent distribution. On a point of detail, writing $1/n, ..., n/n$ implies that a sample can return the maximum possible value of the quantile function, which is impossible for an infinite upper bound. For this reason, sample quantiles are best considered referred to say $(i - a) / (n - 2a + 1)$ for rank $i$ and sample size $n$, with small print disagreements on what $a$ should be. $a = 0.5$ was perhaps the earliest suggestion (Francis Galton). – Nick Cox Dec 07 '20 at 14:09
  • 2
    If the cdf $F$ is strictly increasing and differentiable at the quantile $F^{-1}(p)$ , with derivative $f$, [a CLT applies](https://www.stat.berkeley.edu/~bartlett/courses/2013spring-stat210b/notes/20notes.pdf)$$\sqrt{n}(F_n^-(p)-F^{-1}(p))\stackrel{\mathcal L}{\longrightarrow}\mathcal N(0,p(1-p)/f^2(F^{-1}(p)))$$ – Xi'an Dec 07 '20 at 18:46
  • I guess you're trying to say that as sample size gets higher, the distribution converges to Normal. How about the other way around, any comments on how to improve statistical models that can only depend on small sample size? – develarist Dec 07 '20 at 23:11
  • https://stats.stackexchange.com/q/15891/17230 may be of interest. – Scortchi - Reinstate Monica Dec 11 '20 at 19:34

2 Answers2

4

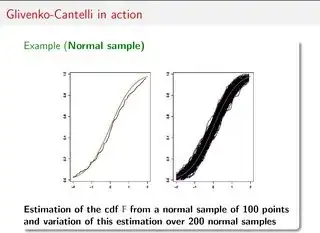
In general, for samples of small or moderate size, a histogram (even with optimal binning and plotted on a 'density scale') need not give a good approximation of the density function of the population. By contrast, an empirical CDF (ECDF), such as you are using, often gives a more reliable view of the population CDF.

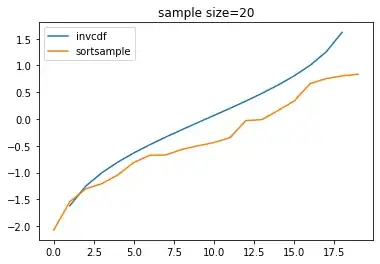
As @NickCox has commented, it is not realistic to expect small samples to give good estimates of CDFs, density functions, or population parameters. In particular, as you have seen, a random sample of size $n = 20$ does not often give useful estimates of characteristics of the population.

Suppose you are interested in a population that happens to be $\mathsf{Norm}(\mu = 100, \sigma = 15).$ Let's look at a sample of size $n= 50.$ Then 95% CIs for $\mu$ and $\sigma$ are $(94.18,103.50)$ and $(13.56, 20.23),$ respectively. [Sampling and computations in R.]

set.seed(1207)
x = rnorm(50, 100, 15)
ci.mu = mean(x) + qt(c(.025,.975),49)*sd(x)/sqrt(50); ci.mu
[1]  94.17782 103.40368
ci.sg = sqrt(49*var(x)/qchisq(c(.975,.025),49));  ci.sg
[1] 13.55869 20.22656

A histogram of the data, the density function of the population (black) and a kernel density estimator of that density (dotted red) are shown below.

hist(x, prob=T, col="skyblue2", main="n = 50")
 rug(x)
 curve(dnorm(x, 100, 15), add=T, lwd=2)
 lines(density(x), col="red", lty="dotted", lwd=2)

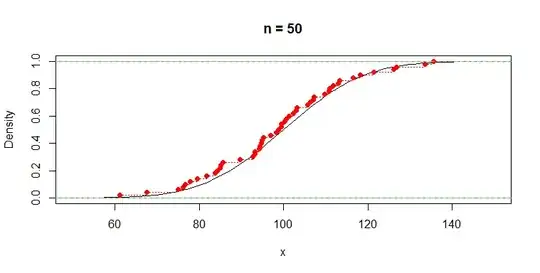
enter image description here

Here are plots of the population CDF and the sample ECDF (red).

curve(pnorm(x, 100, 15), 50, 150, ylab="Density", main="n = 50")
 abline(h=0:1, col="green2")
 lines(ecdf(x), col="red", lty="dotted")

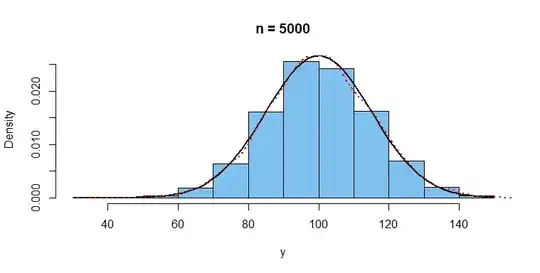
enter image description here

With a sample of size $n = 5000,$ we get a much better view of the population distribution.

set.seed(1207)
y = rnorm(5000, 100, 15)
ci.mu = mean(y) + qt(c(.025,.975),4999)*sd(y)/sqrt(5000); ci.mu
[1]  99.74097 100.57105
ci.sg = sqrt(4999*var(y)/qchisq(c(.975,.025),4999));  ci.sg
[1] 14.68228 15.26937

hist(y, prob=T, col="skyblue2", main="n = 5000")
 curve(dnorm(x, 100, 15), add=T, lwd=2)  # syntax requires 'x'
 lines(density(y), col="red", lty="dotted", lwd=2)

enter image description here

The population density (black) and the ECDF (red) are difficult to distinguish.

curve(pnorm(x, 100, 15), 50, 150, lwd=2, ylab="Density", main="n = 5000")
 abline(h=0:1, col="green2")
 lines(ecdf(y), col="red", lty="dotted")

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • so there are no bias tricks, sampling or estimation techniques, or modifications to the CDF that can improve a small-sample statistical model? meaning there is no hope in estimating a model that is doomed to have small sample size to begin with, in other words, futile, and the user has too high standards? – develarist Dec 07 '20 at 23:12
  • 3
    Not saying $n = 50$ observations tell you _nothing._ But use as large an $n$ is needed to decide issues important to you. Possible waste of time/energy/money to do a study with too small an $n.$ There are 'sample size' procedures for intelligent speculation about how large $n$ needs to be in order to get useful results for your purpose. // In a real expt (instead of a simulation) it _might_ be good enough to know $\mu$ is btw 94 and 104. (For example, If you need $\mu = 120$ for a profitable product, you can scrap plans for this one and try to get a better idea.) – BruceET Dec 07 '20 at 23:14
2

In complement to BruceET's full answer, here are two slides from my undergraduate mathematical statistics course this trimester:

                  enter image description here

The first slide shows (left) one realisation of an empirical cdf for a Normal sample of size $n=100$ when compared with the truth and (right) the variability of an empirical cdf as a random curve for a Normal sample of size $n=100$ when repeated 100 times. I use this experiment to tell my students one can learn a lot from the sample itself without making any assumption on its distribution. In other words and contrary to the OP impression, the performances of the empirical cdf are far from being poor.

                  enter image description here

The second slide shows (left) one realisation of an empirical cdf for a Normal sample of size $n=100$ when compared with the truth and with a Normal cdf using the estimated mean; and (right) the range of variability of an empirical cdf for a Normal sample of size $n=100$ over 100 repetitions, compared with the variability of a parametric estimate of the cdf. I use this experiment to tell my students that the additional item of information about the functional form of the distribution helps in making inference about this distribution (if not misspecified).

The CLT $$\sqrt{n}(F_n^-(p)-F^{-1}(p))\stackrel{\mathcal L}{\longrightarrow}\mathcal N(0,p(1-p)/f^2(F^{-1}(p)))$$ gives the scale of the variability of the empirical inverse cdf $F_n^{-1}$ (that is, the horizontal variability in the above pictures) as the standard deviation at the $p$-quantile of the distribution is of order $$\dfrac{\sqrt{p(1-p)}}{\sqrt nf(F^{-1}(p))}$$ In the case of a Normal sample of size $n=100$, when $p=1/2$, this standard deviation is $$\dfrac{1}{2\times 10\times 1/\sqrt{2\pi}}\approx 0.125$$ which gives a range of $\pm1/4$ on the location of the median.

Xi'an
  • 90,397
  • 9
  • 157
  • 575
  • So to compensate for small sample size, one can replicate the sample 200 times from a matching parametric distribution and use the average of those replications as a reliable model instead of the original empirical sample itself? – develarist Dec 12 '20 at 15:38
  • @develarist: no this is not what this means, in the slide the 200 replications are used to demonstrate the variability under controlled conditions, namely when one already know the distribution of the model. In a _statistical framework_, there is one and only one sample. Repeating this sample by bootstrap provides a measure of variability, but its quality deteriorates as the sample size $n$ decreases. – Xi'an Dec 12 '20 at 16:42
  • (Mentioning bootstrap in my comment above may actually prove confusing as the primary argument supporting bootstrap is exactly the convergence of the empirical cdf to the true cdf. If the approximation by the ecdf is poor, then the bootstrap evaluation will be poor as well.) – Xi'an Dec 12 '20 at 16:50