I have survey data where the outcome is the proportion of a research budget interviewees wished to assign to one of three different "types" of research into solutions for various issues. I am investigating how this proportion varies with the issue's importance, how happy interviewees are with existing solutions, and some additional continuous metrics relating to existing research. I have also included another research type as a fixed factor to account for how changes in the proportion of the budget assigned to other options changes the proportion assigned to the choice of interest (I originally included both alternative research types but they are highly correlated so I have dropped one).
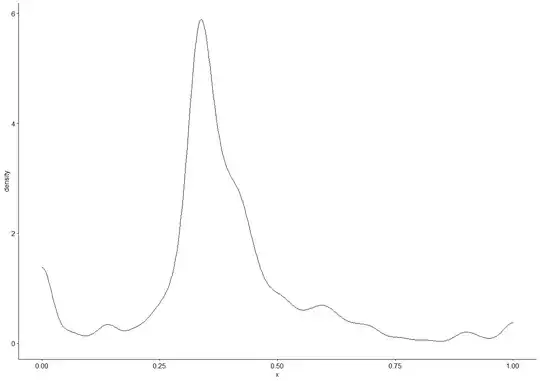
The sample size is 372, and the range is 0-1. The frequency distribution of the data is as follows (most answers were equal distribution of 1/3 of budget to all three options):
To analyse this I have fitted a beta glmm. To address 0s in the dataset I have included a hurdle component and to address the 1s I have multiplied the data by *0.99. Since each interviewee answered this question for multiple issues and the data has been pooled, issue and interviewee are included as random factors. The model formula is as follows:
m1 <- glmmTMB("research type" ~ "issue importance" + "solution satisfaction" + x2 + x3 + x4 * x5 + (1|Issue) + (1|Interviewee),
data = X,
ziformula =~.,
family= beta_family())
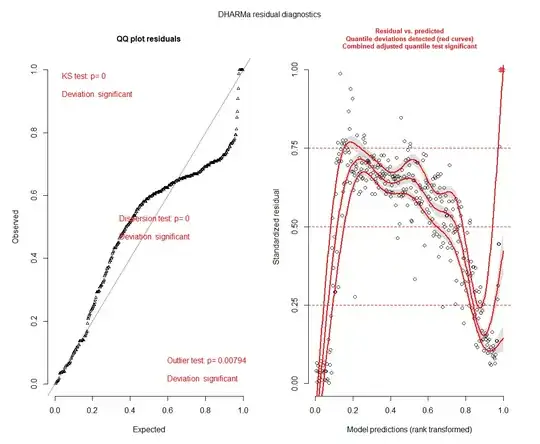
When I went to check my model fit with DHARMa and plotted the residuals, I obtained the following output:
library(DHARMa)
simulateResiduals(m1, plot = T)
A test of dispersion confirms the model is under/overdispered
testDispersion(m1)
DHARMa nonparametric dispersion test via sd of residuals fitted vs. simulated
data: simulationOutput
ratioObsSim = 0.27802, p-value < 2.2e-16
alternative hypothesis: two.sided
Now, my understanding is that since I am using beta distribution, under/overdispersion per se doesn't matter since the dispersion can vary, but this still seems like a bad fit, but while there is lots of information on how to address overdispersion, I am unable to find any suggestions on how to address this sort of deviation from the fit. Should I be worried and, if so, how can I address it?