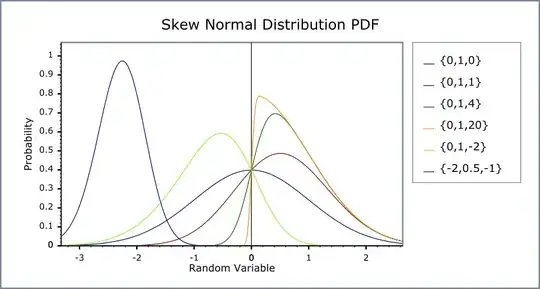
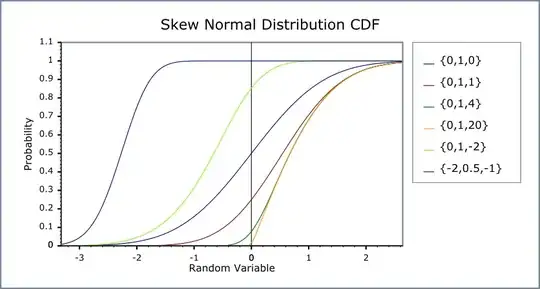
The following two figures are the pdf's of four parametric distributions and their corresponding cdf's. The most left-ward blue line is clearly not skewed, while the most right-ward orange line is positively skewed.
It is very easy to see which pdf's are positively skewed, but not so apparent in their corresponding cdf's. The blue and orange cdf's have virtually the same curvature. (Note that a dataset containing all negative values could still have a positive skew in its distribution, so the position of a distribution on the real-number line is not indicative of skewness whatsoever.)
Are there tell-tale signs from a cdf's plot, or underlying statistics (without knowing the parameters of how they were constructed of course), that are clear give-aways as to a cdf being positively skewed?