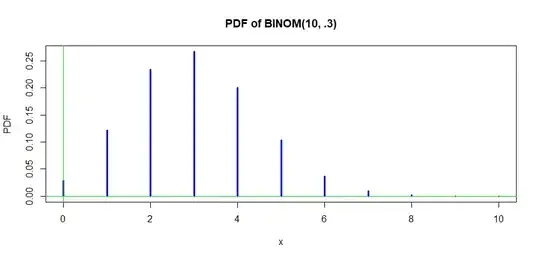
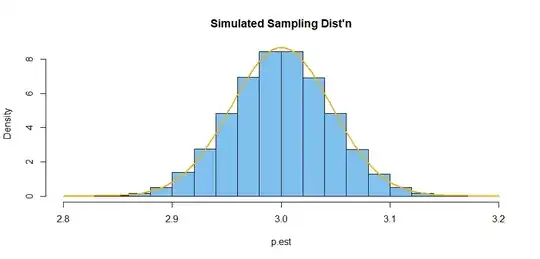
I'm looking for a simple answer to this question relating the central limit theorem and Gaussian and skewed distributions, if one exists. I used the binomial function to generate calculations of the probabilities of possible outcomes for 10 flips of an unfair coin (p=0.3, q=0.7) and obtained a skewed distribution. I have been thinking of this as a kind of sampling distribution of proportions. If the coin was flipped 10 trillion times, with 3 trillion heads and 7 trillion tails, and 10 flip samples are plotted into the sampling distribution, yielding my skewed curve.
Now I also "learned" that the central limit theorem says that the sampling distribution of any distribution is a Gaussian curve, but I acknowledge that that my studies of this are relatively superficial. Is a skewed curve still considered a Gaussian curve? Are there other important aspects about the central limit theorem that I am clearly unaware of? I'm not looking for a comprehensive explanation necessarily, but just some guidance about misconceptions that I may have.
Thanks.