Unpooling standard deviation from a combined set and a subset

Question

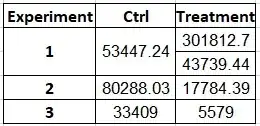
I do not have access to the original data set.

AB: Overall mean: 149.41 sd: 89.13 N: 2284

B: Subset mean: 110.98 sd: 73.53 N: 917

I need to determine the original mean and standard deviation or variance of the original A set that is combined in the set AB

In order to determine the mean of A given sd, and N of AB and B we can do:

mean(AB-B) = (149.41*2284 - 110.98*917)/(2284-917) = 175.19

Is it possible to determine the standard deviation or variance of the set AB=(AB-B) given the limited data?

Update: @WHuber suggested @Ben's post https://stats.stackexchange.com/a/384951/70282 which suggests:

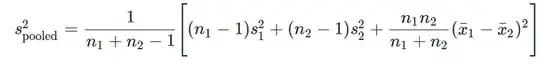
I converted that to R, tested it and indeed it works.

pooledSD=function(n1,n2,m1,m2,s1,s2) {  
  sqrt( 1/(n1+n2-1)*( (n1-1)*s1^2 + (n2-1)*s2^2 + (n1*n2)/(n1+n2)*(m1-m2)^2))
}

Testing the above on a synthetic data works perfectly for the union of sets.

Using algebra and solving for s1^2, I get:

I tested the above function now and it works!

P.S. I appreciate the additional background that Ben gives below.

Answer 1

(I am certainly glad the variance decomposition formula in O'Neill (2014) is working correctly!) It is possible to produce a general formula for this problem and implement it as a new function in R. First we write the equation for the unknown mean:

$$\begin{align} \bar{x}_{A} = \frac{\dot{x}_A}{n_A} = \frac{\dot{x}_{AB} - \dot{x}_B}{n_{AB}-n_B} &= \frac{n_{AB} \cdot \bar{x}_{AB} - n_{B} \cdot \bar{x}_B}{n_{AB}-n_B}. \\[6pt] \end{align}$$

Now we can substitute this equation into the equation for the unknown variance to get:

$$\begin{align} s_{A}^2 &= \frac{1}{n_A-1} \Bigg[ (n_A+n_B-1) s_{AB}^2 - (n_B-1) s_B^2 - \frac{n_A n_B}{n_A + n_B} (\bar{x}_A - \bar{x}_B)^2 \Bigg] \\[6pt] &= \frac{1}{n_{AB}-n_B-1} \Bigg[ (n_{AB}-1) s_{AB}^2 - (n_B-1) s_B^2 - \frac{(n_{AB}-n_B) n_B}{n_{AB}} (\bar{x}_A - \bar{x}_B)^2 \Bigg] \\[6pt] &= \frac{1}{n_{AB}-n_B-1} \Bigg[ (n_{AB}-1) s_{AB}^2 - (n_B-1) s_B^2 \Bigg] \\[6pt] &\quad - \frac{1}{n_{AB}-n_B-1} \Bigg[ \frac{(n_{AB}-n_B) n_B}{n_{AB}} \Big( \frac{n_{AB} \cdot \bar{x}_{AB} - n_{B} \cdot \bar{x}_B}{n_{AB}-n_B} - \bar{x}_B \Big)^2 \Bigg] \\[6pt] &= \frac{1}{n_{AB}-n_B-1} \Bigg[ (n_{AB}-1) s_{AB}^2 - (n_B-1) s_B^2 \Bigg] \\[6pt] &\quad - \frac{1}{n_{AB}-n_B-1} \Bigg[ \frac{(n_{AB}-n_B) n_B}{n_{AB}} \Big( n_{AB} \cdot \frac{\bar{x}_{AB} - \bar{x}_B}{n_{AB}-n_B} \Big)^2 \Bigg] \\[6pt] &= \frac{1}{n_{AB}-n_B-1} \Bigg[ (n_{AB}-1) s_{AB}^2 - (n_B-1) s_B^2 - \frac{n_{AB} \ n_B}{n_{AB}-n_B} ( \bar{x}_{AB} - \bar{x}_B )^2 \Bigg]. \\[6pt] \end{align}$$

We can program this formula into R as follows:

VARDIFF <- function(n.pool, mean.pool, var.pool, n.sub, mean.sub, var.sub) {
  
  T1 <- (n.pool-1)*var.pool
  T2 <- (n.sub-1)*var.sub
  T3 <- ((n.pool*n.sub)/(n.pool-n.sub))*(mean.pool - mean.sub)^2
  
  (T1 - T2 - T3)/(n.pool-n.sub-1) }

For your particular example you get:

var.A <- VARDIFF(n.pool = 2284, mean.pool = 149.41, var.pool = 89.13^2, 
                 n.sub  =  917, mean.sub  = 110.98, var.sub  = 73.53^2)

var.A
[1] 7995.061

sqrt(var.A)
[1] 89.4151

As you can see, in your particular problem you have $s_A^2 =7995.061$ and $s_A = 89.4151$.

Answer 2

Use the sample.decomp function in the utilities package

Statistical problems of this kind have now been automated in the sample.decomp function in the utilities package. This function can compute pooled sample moments from subgroup moments, or compute missing subgroup moments from the other subgroup moments and pooled moments. It works for decompositions up to fourth order ---i.e., decompositions of sample size, sample mean, sample variance/standard deviation, sample skewness, and sample kurtosis.

---

How to use the function: Here we give an example where we use the function to compute the sample moments of the missing subgroup with your data. As you can see from the code below, we input the sample sizes, sample means and sample standard deviations into the function, and we specify which group is the pooled group. The output shows the moments for all the groups, including the missing subgroup.

#Show sample statistics for the subgroups
library(utilities)
N      <- c(2284, 917)
MEAN   <- c(149.41, 110.98)
SD     <- c(89.13, 73.53)

#Compute sample decomposition
sample.decomp(n = N, sample.mean = MEAN, sample.sd = SD, 
              names = c('AB', 'A'), pooled = 1, include.sd = TRUE)

              n sample.mean sample.sd sample.var
A           917    110.9800   73.5300   5406.661
--other--  1367    175.1893   89.4151   7995.061
--pooled-- 2284    149.4100   89.1300   7944.157

You can read about this function in the package documentation. The function allows computation of sample moments up to fourth order (mean, variance, skewness and kurtosis).