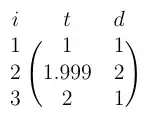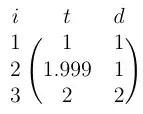1

I'm looking to calculate the exponential moving average & exponential moving variance of a continuous series of request/responses, using each response's duration and the interval (time delta) since the previous response.

Since the only pieces of information we have are response duration & timestamp, but we want concurrency, we can use $concurrency = rate \cdot duration$. And we can derive instantaneous $rate$ as $rate = 1 / \Delta t$.

For EWMA & EWMV, we'll use irregular weighted versions of EWMA 1 2 and EWMV 1 2. Weighting based on $\Delta t$ should smooth out the extreme values produced by $rate = 1/\Delta t$.

Putting it all together we have:

$r_i = 1 / (t_i - t_{i-1})$

$x_i = r_i \cdot d_i$

$\alpha_i = 1 - e^{-(t_i - t_{i-1})/\tau}$

$\mu_i = \mu_{i-1} + \alpha_i(x_i - \mu_{i-1})$

$\sigma_i = (1 - \alpha) (\sigma_{i-1} + \alpha (x_i - \mu_{i-1})^2)$

Where

  • $t_i$ is the timestamp of the response
  • $d_i$ is the request/response duration
  • $r_i$ is the instantaneous rate
  • $x_i$ is the instantaneous concurrency of the response
  • $\tau$ is the time constant or window size
  • $\mu_i$ is the EWMA of the concurrency
  • $\sigma_i$ is the EWMV of the concurrency

Lets look at some examples where we know approximately what the results should be.

To start, lets assume we've started with an extremely steady concurrency, with average 2, and 0 variance. Let $\tau = 2$, $t_0 = 0$, $\mu_0 = 2$, and $\sigma_0 = 0$.
We then receive the following samples:

matrix1

So we had 2 requests at $t=1$ and $t=2$ with $duration=1$, and another request slightly before the end at $t=1.999$ with $duration=2$. So effectively for the entire time period between $t=0$ and $t=2$ the concurrency was $\approx2$.
However when we run the calculations we come up with:

$\mu_4 = 2.367523$
$\sigma_4 = 1995.998844$

We should have expected $\mu_4 \approx 2$ and $\sigma_4 \approx 0$

Lets look at another example. Since the last 2 samples ($i=2$ & $i=3$) were nearly simultaneous, we should be able to flip them around without changing the result much.

matrix2

This results in:

$\mu_4 = 2.261011$
$\sigma_4 = 498.048046$

Again, both values are higher than they should be, $\sigma$ is radically different, and even $\mu$ has a greater difference than there should be.

Where I believe this is breaking down is in the calculation of $x_i$. While $r_i$ is the instantaneous rate, $d_i$ is not an instant.
When $\Delta t$ is very small, $r_i$, and $x_i$ become very large. Now $\alpha_i$ is playing a part in scaling this back down since it's based off $\Delta t$, but obviously not enough.

So my question is: What is the proper way to accomplish this?
I would guess that when calculating rate, the duration needs to be scaled down with some exponential relation to $\tau$ and $\Delta t$, but not sure what that should be. I also don't want to rely on having to smooth it out too much or that kinda defeats the point of calculating the variance. I realize none of this is going to be exact, just need to be able to figure out what reasonable bounds for real concurrency should be.

phemmer
  • 111
  • 4
  • Hi: I didn't read the actual details behind the problem so carefully but you are using a smoothing constant that is changing during each period. Maybe this is a different type of EWMA application but in all the ones that I'm familiar with, the smoothing parameter is fixed and not changing during each period. Also, EWMA needs some kind of "burn in " period so your sample size is too small. Hopefully someone else can say something else that is more application related. – mlofton Nov 20 '20 at 03:10
  • A constant smoothing factor only applies when your time delta is constant. Mine is not. I provided links to multiple sources using the same algorithm I am. Yes, the "burn in" consideration is explained by the statement "lets assume we've started with an extremely steady concurrency, with average 2, and 0 variance.". Essentially I provided EMA_0, so warmup is addressed. – phemmer Nov 20 '20 at 03:26
  • Hi Patrick. I missed the links because I tread quickly. I'll have to read them when I get more time because I work EWMA a lot but only in constant time-step. Obviously, if the algorithm is really incorporating your steady state assumptions, then the variance clearly shouldn't jump like that. But, the steady state is then dependent on on time delta so that gets confusing. My apologies for not useful comments. It does sound like an interesting problem. – mlofton Nov 20 '20 at 13:44
  • Patrick: I just looked at the EWMA links and, as far as I can tell, when an observation gets very, very close to a previous observation IN TIME, then its weight in terms of the calculation of the weighted moving average goes towards 1.0. That's not intuitive to me ( why would one want to do that ? ) but if that makes sense in the context of what you're doing, then maybe your jumps in $\sigma$ are consistent with that behavior. – mlofton Nov 20 '20 at 13:59
  • "why would one want to do that ?" -- Lets say your time constant is 5 minutes. But instead of getting a sample every 1 minute, one of your samples comes in a few seconds after the previous one. If you apply it with the same scaling factor, then it'll calculate as if the sample came in 1 minute later, not a few seconds. Thus you have to reduce the scaling factor so you're not over-weighting the sample. If you have further questions, lets continue in chat so we're not cluttering up the question's comments. – phemmer Nov 20 '20 at 14:09
  • Hi Patrick: sure we can continue in chat but, by that approach, if an observation, x, comes in immediately after a previous one, then you give it all the weight ( and no weight to anything else ). That doesn't make sense if you ask me because what makes that obs so important compared to the others that it gets all the weight. Yes, the obs's weight could possibly be modified but not to such extreme values. I would think that, if an obs comes in more quickly than expected, then give it the similar weight that the previous one next to it received rather than weight it towards 1.0. – mlofton Nov 21 '20 at 19:08

0 Answers0