1

Assuming I have $$X_1,X_2,...,X_{100}\sim N(1,4)$$ and $$Y_1,Y_2,...,Y_{20}\sim N(2,9)$$ where all $X$ are iid, all $Y$ are iid.

Then should $$\text{var}(X_1+X_2+\ldots+X_{100}+Y_1+\ldots + Y_{20}) = 100 \times 4 + 20 \times 9$$ or $$\text{var}(X_1+X_2+\ldots+X_{100}+Y_1+\ldots + Y_{20})=100^2* \times 4 + 20^2 \times 9$$ ?

Kolmogorov
  • 571
  • 3
  • 15
Stat_newbie
  • 11
  • 1
  • https://stats.stackexchange.com/search?q=variance+sum+formula – whuber Nov 14 '20 at 21:41
  • Replace "100" by "2", focus on the $X_i$ alone, and apply the formula (as explained, *inter alia,* at https://stats.stackexchange.com/questions/346327): what does it imply? – whuber Nov 14 '20 at 21:43

2 Answers2

1

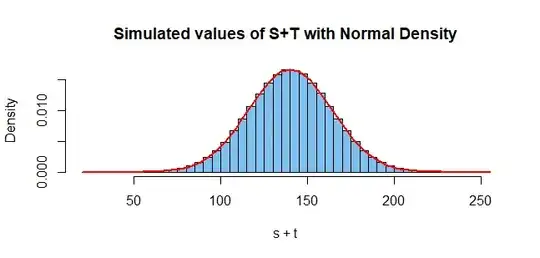
(1) Let $S = \sum_i X_i.$ Then $Var(S) = \sum_i Var(X_i) = 100(4) = 400$, by independence, assuming your notation means $Var(X_i) = 4.$ Similarly, $T = \sum_i Y_i$ has $Var(T) = 20(9)= 180.$ So assuming the $X_i$ are independent of the $Y_i,$ you have $Var(S+T) = 400+180 = 580.$

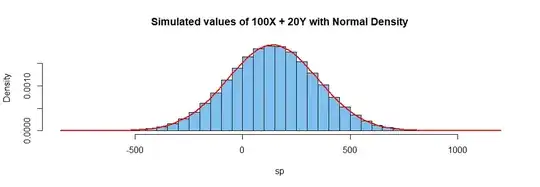
(2) By contrast, if $X \sim \mathsf{Norm}(\mu=1, \sigma=2),$ you have $Var(100X)$ $= 100^2Var(X)$ $= 40000.$ And if, independently $Y \sim\mathsf{Norm}(\mu=2,\sigma=3),$ then $Var(20Y) = 20^2Var(Y)$ $= 400(9)$ $= 3600.$ Then $Var(100X + 20Y) = 40000 + 3600 = 43600.$

Simulation of (1): Notice that the third argument of rnorm is the population standard deviation. With a million iterations, one can expect about two significant digits of accuracy for variances, which have squared units.

set.seed(1114)
s = replicate( 10^6, sum(rnorm(100, 1, 2)) )
t = replicate( 10^6, sum(rnorm(20, 2, 3)) )

mean(s); mean(t);  mean(s+t)
[1] 100.0397    # aprx E(S) = 100(1) = 100
[1] 40.0168     # aprx E(T) = 20(2_ = 40
[1] 140.0565    # aprs E(S+T) = 140

var(s);  var(t);  var(s+t)
[1] 398.7767   # aprx Var(S) = 400
[1] 180.19     # aprx Var(T) = 180
[1] 579.8212   # aprx Var(S+T) = 580

hdr = "Simulated values of S+T with Normal Density"
hist(s+t, prob=T, br=50, col="skyblue2", main=hdr)
 curve(dnorm(x, 140, sqrt(580)), add=T, col="red", lwd=2)

enter image description here

(2) Simulated:

set.seed(2020)
x = rnorm(10^6, 1, 2)
px = 100*x
y = rnorm(10^6, 2, 3)
py = 20*y
sp = px + py
mean(px);  mean(py);  mean(sp)
[1] 100.1081    # aprx E(100X) = 100(1) = 100
[1] 39.92436    # aprx E(20Y) = 20(2) = 40
[1] 140.0325    # aprx(E(100X + 20Y) = 100 + 40 = 140
var(px);  var(py);  var(sp)
[1] 39936.98    # aprx Var(100X) = 10000(4) = 40000
[1] 3601.973    # aprx Var(20Y) = 400(9) = 3600
[1] 43521.24    # aprx Var(100X + 20y) = 43600

hdr = "Simulated values of 100X + 20Y with Normal Density"
hist(sp, prob=T, br=50, col="skyblue2", main=hdr)
 curve(dnorm(x, 140, sqrt(43500)), add=T, col="red", lwd=2)

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • So, which is correct if we want to calculate the variance of sum of all variables? – Stat_newbie Nov 14 '20 at 23:59
  • The sum of all variables is $S+T,$ so the first answer is correct. // My second answer was to show that _your_ second proposed answer is for something different. // Summing 100 independent random variables from the same populations is not the same thing as multiplying _one_ such random variable by 100. – BruceET Nov 15 '20 at 00:02
  • 1
    So is it correct to say that if we follow (2), the variables are NOT independent, as in it is simply X_1 summed 100 times, plus Y_1 summed 20 times? – Stat_newbie Nov 15 '20 at 00:06
  • Right. Multiplying a variable by 100 (that, is adding the same value 100 times) is not the same thin as adding 100 independent random variables. – BruceET Nov 15 '20 at 00:33
1

It holds that: $$ Var \left [ \sum_{i=1}^nX_i \right ] = \sum_{i=1}^n \sum_{j=1}^n Cov \left [ X_i, X_j \right ] $$

If $X_i$ are independent (identical distribution not needed) (assuming variances exist and are finite) then $Cov[X_i,X_j] = 0$ for all $i \ne j$. Thus the formula above simplifies to: $$ Var \left [ \sum_{i=1}^nX_i \right ] = \sum_{i=1}^n \sum_{j=1}^n Cov \left [ X_i, X_i \right ] = \sum_{i=1}^n Var \left [ X_i \right ] $$

Thus, for independent random variables, the variance of the sum is the sum of the variances, i.e. in your case: $4 + 4 + ... + 9 + 9 + ... = 4 * 100 + 9*20$.

Tip:

You are confusing the number of elements in the sum with the weights of the elements. If you have a weighted sum, then the formula for the variance of the sum changes by needing to multiply each individual variance with the squared weight. For example, in 2-variable case (still assuming $X1 \perp \! \! \! \perp X_2$, i.e. independence):

Not weighted sum (your case): $Var[X_1 + X_2] = Var[X_1] + Var[X_2]$

Weighted sum: $Var[w_1 X_1 + w_2 X_2] = w_1^2 Var[X_1] + w_2^2 Var[X_2]$

Note how in your example you have no weights (or weights of 1), so no need to square anything.

PaulG
  • 793
  • 2
  • 10