2

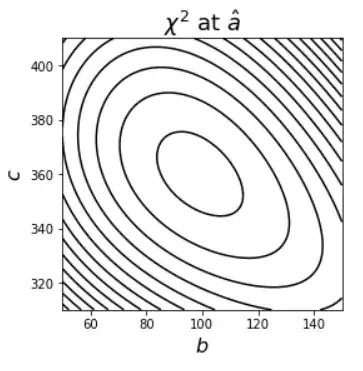
I am using the method of least squares to estimate parameter values for a nonlinear model with three parameters: $a$, $b$, and $c$. Call the sum of the squares of the residuals $\chi^2$. I plot $\chi^2$ as a function of $b$ and $c$ at the minimizing value of $a=\hat{a}$. For a particular data set, this looks as follows:

enter image description here

Naively, I would say that $b$ and $c$ are negatively correlated; e.g., it looks like if one is increased, the other must decrease to "keep $\chi^2$ small". However, a numerical estimate of the covariance matrix says that $\mathrm{cov}(b, c) > 0$. (I have calculated this a number of ways and the sign is always positive.) I am confused by this.

I think my misunderstanding may have something to do with the law of total covariance. That is:

$$\mathrm{cov}(b, c) = \mathrm{E}[\mathrm{cov}(b, c | a)] + \mathrm{cov}[\mathrm{E}(b|a), \mathrm{E}(c|a)]$$

Perhaps the plot I have made is only showing me $\mathrm{E}[\mathrm{cov}(b, c | a)]$ and the other term on the right-hand-side is positive and larger in magnitude, resulting in $\mathrm{cov}(b, c) > 0$.

Can someone verify if this is (or isn't) the case, and perhaps shed a little light on why one cannot (or can) look at the above plot the way I am trying to?

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
aFo23
  • 31
  • 3
  • 1
    If two variables are positively correlated, their regression parameters will be negatively correlated. (W/ 3+ variables, it gets more complicated.) This is completely to be expected. It doesn't have anything to do w/ OLS or nonlinear regression. – gung - Reinstate Monica Nov 11 '20 at 17:55
  • Thank you for your reply, but I am afraid I don't quite understand your point. Can you perhaps provide a link to some reference having to do with your first sentence, or how this relates to my question? I apologize for my lack of familiarity with these topics. – aFo23 Nov 11 '20 at 18:09
  • Suppose I want to regress Y on height & weight. H&W are positively correlated. The sampling distribution of the regression slopes for H&W will be negatively correlated. That will be true if I use some other method than OLS, or if this were a logistic regression, etc. – gung - Reinstate Monica Nov 11 '20 at 18:15
  • How exactly are you estimating the covariance matrix of the parameter estimates? – whuber Nov 11 '20 at 18:18
  • To gung: thank you for your response. Perhaps I should have stated this above, but I have only one independent variable. To whuber: I am doing it two ways. The first is using the curve_fit function in scipy in Python, which estimates the Hessian in some way that I don't know the details of. The second way is by calculating the Hessian explicitly for my model. In both methods these approximate the inverse of the covariance matrix, so they are inverted to get the covariance matrix. – aFo23 Nov 11 '20 at 18:28

1 Answers1

1

I think I have found the answer: no, one may not look at the above plot and try to "read off" the sign of the covariance. It is more complicated than that. If the data are Gaussian, then $\chi^2$ is connected to the log-likelihood function as

$$\chi^2(\theta) = -2 \, \mathrm{ln} L(\theta) + \mathrm{constant}$$

In the limit of infinite data, the likelihood function takes on the form of a normal distribution in the fit parameters $\theta$. In the special case of three fit parameters, this is the trivariate normal distribution. The argument of the exponential can be viewed as describing various ellipses, and one can work out the angles their major axes make to the axis of interest. For the special case of unit variance and zero mean, the ellipse in the $\theta_1 - \theta_2$ plane has angle

$$ \phi = \tan^{-1} \left[ \frac{(\rho_{23}^2-\rho_{13}^2) - \sqrt{(\rho_{23}-\rho_{13})^2 + 4(\rho_{13}\rho_{23}-\rho_{12})^2} }{2(\rho_{13}\rho_{23}-\rho_{12})}\right]$$

where the $\rho_{ij}$ are the correlations. (Identical to the covariance in this case.) For plots of $\phi$ in the $\rho_{13} - \rho_{23}$ plane at various values of $\rho_{12}$, one can see that the angle of the ellipse changes sign depending on the values of $\rho_{13}$ and $\rho_{23}$.

aFo23
  • 31
  • 3