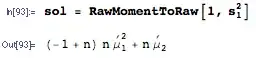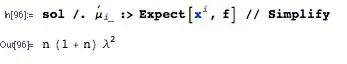12

If $X_i$ is exponentially distributed $(i=1,...,n)$ with parameter $\lambda$ and $X_i$'s are mutually independent, what is the expectation of

$$ \left(\sum_{i=1}^n {X_i} \right)^2$$

in terms of $n$ and $\lambda$ and possibly other constants?

Note: This question has gotten a mathematical answer on https://math.stackexchange.com/q/12068/4051. The readers would take a look at it too.

Community
  • 1
Isaac
  • 973
  • 1
  • 9
  • 20
  • 5
    The two copies of this question reference each other and, appropriately, the stats site (here) has a statistical answer and the math site has a mathematical answer. It seems like a good division: let it stand! – whuber Mar 04 '11 at 21:59

3 Answers3

31

If $x_i \sim Exp(\lambda)$, then (under independence), $y = \sum x_i \sim Gamma(n, 1/\lambda)$, so $y$ is gamma distributed (see wikipedia). So, we just need $E[y^2]$. Since $Var[y] = E[y^2] - E[y]^2$, we know that $E[y^2] = Var[y] + E[y]^2$. Therefore, $E[y^2] = n/\lambda^2 + n^2/\lambda^2 = n(1+n)/\lambda^2$ (see wikipedia for the expectation and variance of the gamma distribution).

Wolfgang
  • 15,542
  • 1
  • 47
  • 74
  • Thanks. A very neat way of answering the question (leading to the same answer) was also provided on math.stackexchange (link above in the question) a few minutes ago. – Wolfgang Nov 27 '10 at 17:24
  • 2
    The math answer computes the integrals using linearity of expectation. In some ways it's simpler. But I like your solution because it exploits *statistical* knowledge: because you know a sum of independent Exponential variables has a Gamma distribution, you're done. – whuber Nov 27 '10 at 21:19
  • 1
    I enjoyed it quite a bit and I am by no means a statistician or a mathematician. – Kortuk Nov 29 '10 at 18:04
  • very elegant answer. – Cyrus S Nov 30 '10 at 16:44
  • @whuber I don't understand what distinction between _statistical_ knowledge and _mathematical_ knowledge you are trying to draw in your comment. _Somewhere_ one needs to do an integration to compute expectations, or to know a trustworthy source where someone else's results on $E[X]$ and $E[X^2]$ can be looked up (statistical knowledge?), whether it is of a Gamma random variable or the exponential random variable as Macro used. Also, is it possible to _prove_ the result that $\text{var}(Y) = E[Y^2] - (E[Y])^2$ that Wolfgang used without using the linearity of expectation? – Dilip Sarwate Jul 02 '12 at 18:42
  • 1
    @Dilip The mathematician tends to see this question as asking for an integral and proceeds directly to integrate it. The statistician re-expresses it in terms of familiar statistical quantities, such as the variance, and familiar statistical relationships, such as that the Exponential is Gamma and the Gamma family is closed under convolution. The answers are the same but the approaches are completely different. Then there's the question of what "doing an integration" really means. For example, [this complicated integral](http://math.stackexchange.com/a/3972) is done purely algebraically. – whuber Jul 02 '12 at 18:52
10

The answer above is very nice and completely answers the question but I will, instead, provide a general formula for the expected square of a sum and apply it to the specific example mentioned here.

For any set of constants $a_1, ..., a_n$ it is a fact that

$$ \left( \sum_{i=1}^{n} a_i \right)^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} $$

this is true by the Distributive property and becomes clear when you consider what you're doing when you calculate $(a_1 + ... + a_n) \cdot (a_1 + ... + a_n)$ by hand.

Therefore, for a sample of random variables $X_1, ..., X_n$, regardless of the distributions,

$$ E \left( \left[ \sum_{i=1}^{n} X_i \right]^2 \right) = E \left( \sum_{i=1}^{n} \sum_{j=1}^{n} X_i X_j \right) = \sum_{i=1}^{n} \sum_{j=1}^{n} E(X_i X_j)$$

provided that these expectations exist.

In the example from the problem, $X_1, ..., X_n$ are iid ${\rm exponential}(\lambda)$ random variables, which tells us that $E(X_{i}) = 1/\lambda$ and ${\rm var}(X_i) = 1/\lambda^2$ for each $i$. By independence, for $i \neq j$, we have

$$E(X_i X_j) = E(X_i) \cdot E(X_j) = \frac{1}{\lambda^2}$$

There are $n^2 - n$ of these terms in the sum. When $i = j$, we have

$$ E(X_i X_j) = E(X_{i}^{2}) = {\rm var}(X_{i}) + E(X_{i})^2 = \frac{2}{\lambda^2} $$

and there are $n$ of these term in the sum. Therefore, using the formula above,

$$ E \left( \sum_{i=1}^{n} X_i \right)^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} E(X_i X_j) = (n^2 - n)\cdot\frac{1}{\lambda^2} + n \cdot \frac{2}{\lambda^2} = \frac{n^2 + n}{\lambda^2} $$

is your answer.

Macro
  • 40,561
  • 8
  • 143
  • 148
3

This problem is just a special case of the much more general problem of 'moments of moments' which are usually defined in terms of power sum notation. In particular, in power sum notation:

$$s_1 = \sum_{i=1}^{n} X_i$$

Then, irrespective of the distribution, the original poster seeks $E[s_1^2]$ (provided the moments exist). Since the expectations operator is just the 1st Raw Moment, the solution is given in the mathStatica software by:

enter image description here

[ The '___ToRaw' means that we want the solution presented in terms of raw moments of the population (rather than say central moments or cumulants). ]

Finally, if $X$ ~ Exponential($\lambda$) with pdf $f(x)$:

f = Exp[-x/λ]/λ;      domain[f] = {x, 0, ∞} && {λ > 0};

then we can replace the moments $\mu_i$ in the general solution sol with the actual values for an Exponential random variable, like so:

enter image description here

All done.

P.S. The reason the other solutions posted here yield an answer with $\lambda^2$ in the denominator rather than the numerator is, of course, because they are using a different parameterisation of the Exponential distribution. Since the OP didn't state which version he was using, I decided to use the standard distribution theory textbook definition Johnson Kotz et al … just to balance things out :)

wolfies
  • 6,963
  • 1
  • 22
  • 27