2

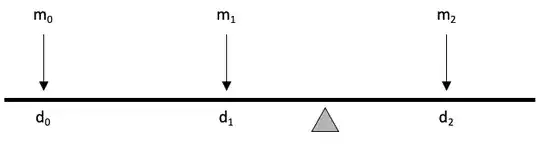
I have three normally distributed random variables $m_0$, $m_1$ and $m_2$, and three fixed values $d_0$, $d_1$ and $d_2$. They represent the physical weights of objects and their placement on a solid bar of any sort. This is a balance point problem. An example is given in the following image:
(example values for additional clarity: $\mu_{m_1}=80kg$, $\sigma_{m_1}=15kg$, $d_1=100cm$)

balance point problem example

I am interested in the nature of the resulting balance point $d$. I assume it to be normally distributed following the normally distributed "weights" $m_i$ with $d \sim N(\mu_d, \sigma_d^2)$.

Generally we know that $$d = \frac{\sum_i{m_i d_i}}{\sum_i{m_i}}$$

applies. It feels natural that the mean of $d$ is

$$\mu_d = \frac{\mu_{m_0} d_0 + \mu_{m_1} d_1 + \ ....}{\mu_{m_0} + \mu_{m_1} + \ ....},$$

however, I find myself not able to figure out the proper way to calculate the standard deviation

$$\sigma_d =\ ....$$

I checked the literature on the sum of normal distributions and the sum of weighted normal distributions. I realize that my problem is different but I can't find the right pointers.

What is the standard deviation (or variance) of the given problem statement?

Edit: Added experiment

I ran an experiment to get a feeling for the problem:

R-Script:

rtznorm <- function(n, m, s, z_limit=1.96) {
  # The normal 'rnorm' function with a limitation of extremes
  sample <- rnorm(n = n, mean = m, sd = s)
  while(any(sample < (m - z_limit * s) | sample > (m + z_limit * s))) {
    sample <- rnorm(n = n, mean = m, sd = s)
  }
  return(sample)
}

cg_x <- function(){
    weights <- rtznorm(n=3, m=80, s=15)
    x_weights <- c(0, 100, 200)
    cgx = sum(weights * x_weights) / sum(weights)
    return(cgx)
}

random_cgx <- replicate(500000, cg_x())
hist(random_cgx)
c(mean(random_cgx), sd(random_cgx))

A random run of the experiment resulted in $\mu= 99.981, \sigma=7.779$ and

Example sample histogram

Mazzen
  • 21
  • 2
  • Except for special values of the $d_i,$ $d$ does not have a mean and therefore has an infinite variance. This follows from the general result at https://stats.stackexchange.com/questions/299722 by expressing $d$ as a sum of random variables, one of which is a ratio of independent Normal variables. Your problem is that it isn't physically meaningful to model weights as Normal variables, because that assigns positive probability to negative weights. Even when that probability is tiny, it creates mathematical problems with the distribution of $d.$ – whuber Nov 09 '20 at 19:28
  • Thanks! That was indeed insightful. Is it still possible to solve my problem under restrictions? My physical weights will always be positiv and the the $d_i$ will always have a mean. I appologize if I chose the wrong community to ask my question. I'm of course interested in the mathematical background but even more so in a way to solve my specific problem. – Mazzen Nov 10 '20 at 09:12
  • You need a more realistic model. Choosing one requires understanding something about how your weights might vary (or about the epistemic uncertainties in their values). Unfortunately, your abstract description of the problem precludes any possibility that we could help you with that. Could you provide some information about this? – whuber Nov 10 '20 at 13:32
  • Hey @whuber, appreciate your help! I added an experiment to the original posting. Curious about what the result of this exercise could look like I approached this from another direction. The shown result looks promising, however, the method is not suited for my use case. I am still in need of a numerical solution. You asked about a realistic model. I am sure there are scientifically better ways to model weight of e.g. people. In the experiment I worked with a limited normal distribution. – Mazzen Nov 19 '20 at 12:50
  • Would it make sense to move my question to a more practically/physics focused StackExchange group? I appreciate your advice in any direction! – Mazzen Nov 19 '20 at 13:00

0 Answers0